题目内容
【题目】如图,已知三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点.
的中点.
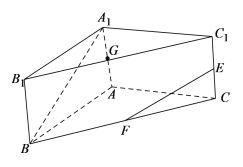
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)若![]() 为线段
为线段![]() 的中点,试在图中作出过
的中点,试在图中作出过![]() 、
、![]() 、
、![]() 三点的平面截该棱柱所得的多边形,并求出以该多边形为底,
三点的平面截该棱柱所得的多边形,并求出以该多边形为底,![]() 为顶点的棱锥的体积.
为顶点的棱锥的体积.
【答案】(1)![]() ;(2)截面见详解,体积为
;(2)截面见详解,体积为![]()
【解析】
(1)连接![]() 交于点
交于点![]() ,根据中位线定理找到与
,根据中位线定理找到与![]() 的平行线
的平行线![]() ,并找到异面直线
,并找到异面直线![]() 与
与![]() 所成角,计算
所成角,计算![]() 长度,根据余弦定理,可得结果.
长度,根据余弦定理,可得结果.
(2)画出截面![]() ,计算四边形
,计算四边形![]() 的面积,根据
的面积,根据![]() //面
//面![]() ,可得
,可得![]() 到面
到面![]() 的距离,结合椎体体积公式,可得结果.
的距离,结合椎体体积公式,可得结果.
(1)连接![]() 交于点
交于点![]() ,连接
,连接![]()
如图

由![]() 底面
底面![]() ,
,![]() 面
面![]() ,
,
所以![]() ,又
,又![]()
所以![]() ,
,![]() 面
面![]()
所以![]() 面
面![]() ,
,
故四边形![]() 为矩形,所以
为矩形,所以![]() 共线
共线
![]() 为
为![]() 的中点,所以
的中点,所以![]() //
//![]() ,
,
故异面直线![]() 与
与![]() 所成角为
所成角为![]()
![]() ,
,![]() ,
,![]() ,
,
且![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点
的中点
所以![]()
所以![]()
又![]() 且
且![]()
所以![]() 为等腰直角三角形,
为等腰直角三角形,
故![]()
(2)取![]() 的中点
的中点![]() 连接
连接![]() ,
,![]()
又![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() //
//![]()
则![]() //
//![]() ,且
,且![]()
过![]() 、
、![]() 、
、![]() 三点的平面截该棱柱
三点的平面截该棱柱
所得的多边形为四边形![]()
由(1)可知,![]() //
//![]() 且
且![]()
所以四边形![]() 为直角梯形,
为直角梯形,
所以
![]()
又![]()
![]() 平面
平面![]() ,
,![]() 面
面![]() ,
,
所以![]() //平面
//平面![]() ,作
,作![]()
所以![]()
且![]() 到截面的距离即
到截面的距离即![]()
所以![]()

【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,记其质量指标值为![]() ,当
,当![]() 时,产品为一级品;当
时,产品为一级品;当![]() 时,产品为二级品;当
时,产品为二级品;当![]() 时,产品为三级品.现用两种新配方(分别称为
时,产品为三级品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做实验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
配方)做实验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
频数 | 10 | 30 | 40 | 20 |
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 5 | 10 | 15 | 30 | 40 |
(1)从![]() 配方生产的产品中按等级分层抽样抽取5件产品,再从这5件产品中任取3件,求恰好取到1件二级品的频率;
配方生产的产品中按等级分层抽样抽取5件产品,再从这5件产品中任取3件,求恰好取到1件二级品的频率;
(2)若这种新产品的利润率![]() 与质量指标
与质量指标![]() 满足如下条件:
满足如下条件: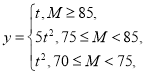 ,其中
,其中![]() ,请分别计算两种配方生产的产品的平均利润率,如果从长期来看,你认为投资哪种配方的产品平均利润率较大?
,请分别计算两种配方生产的产品的平均利润率,如果从长期来看,你认为投资哪种配方的产品平均利润率较大?
【题目】哈三中团委组织了“古典诗词”的知识竞赛,从参加考试的学生中抽出60名学生(男女各30名),将其成绩分成六组![]() ,
,![]() ,…,
,…,![]() ,其部分频率分布直方图如图所示.
,其部分频率分布直方图如图所示.
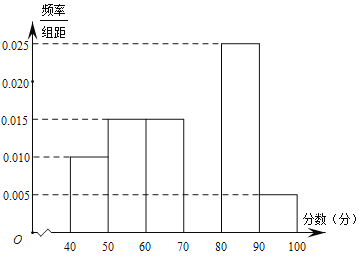
(Ⅰ)求成绩在![]() 的频率,补全这个频率分布直方图,并估计这次考试的众数和中位数;
的频率,补全这个频率分布直方图,并估计这次考试的众数和中位数;
(Ⅱ)从成绩在![]() 和
和![]() 的学生中选两人,求他们在同一分数段的概率;
的学生中选两人,求他们在同一分数段的概率;
(Ⅲ)我们规定学生成绩大于等于80分时为优秀,经统计男生优秀人数为4人,补全下面表格,并判断是否有99%的把握认为成绩是否优秀与性别有关?
优秀 | 非优秀 | 合计 | |
男 | 4 | 30 | |
女 | 30 | ||
合计 | 60 |
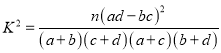
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |




