Question

【题目】设函数f（x）=x3+ax2﹣a2x+1，g（x）=ax2﹣2x+1，其中实数a≠0．
（1）若a＞0，求函数f（x）的单调区间；
（2）当函数y=f（x）与y=g（x）的图象只有一个公共点且g（x）存在最小值时，记g（x）的最小值为h（a），求h（a）的值域；
（3）若f（x）与g（x）在区间（a，a+2）内均为增函数，求a的取值范围．

Answer 1

【答案】
（1）解：∵ ，又a＞0，

∴当 时，f'（x）＞0；

当 时，f'（x）＜0，

∴f（x）在（﹣∞，﹣a）和 内是增函数，在 内是减函数．

（2）解：由题意知x3+ax2﹣a2x+1=ax2﹣2x+1，

即x[x2﹣（a2﹣2）]=0恰有一根（含重根）．∴a2﹣2≤0，即- ≤a≤ ，

又a≠0，∴ ．

当a＞0时，g（x）才存在最小值，∴ ．

g（x）=a（x﹣ ）2+1﹣ ，

∴ ．

h（a）≤1﹣ ；

∴h（a）的值域为 ．

（3）解：当a＞0时，f（x）在（﹣∞，﹣a）和 内是增函数，g（x）在 内是增函数．

由题意得 ，解得a≥1；

当a＜0时，f（x）在 和（﹣a，+∞）内是增函数，g（x）在 内是增函数．

由题意得 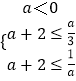，解得a≤﹣3；

综上可知，实数a的取值范围为（﹣∞，﹣3]∪[1，+∞）

【解析】（1）先对函数f（x）进行求导，令导函数大于0可求函数的增区间，令导函数小于0可求函数的减区间．（2）令f（x）=g（x）整理可得x[x2﹣（a2﹣2）]=0，故a2﹣2≤0求出a的范围，再根据g（x）存在最小值必有a＞0，最后求出h（a）的值域即可．（3）分别求出函数f（x）与g（x）的单调区间，然后令（a，a+2）为二者单调增区间的子集即可．
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．