题目内容
 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.(1)若多面体面对角线AC,BD交于点O,E为线段AA1的中点,求证:OE∥平面A1C1C;
(2)若a=4,b=2,求该多面体的体积;
(3)当a,b满足什么条件时AD1⊥DB1,并证明你的结论.
分析:(1)连接AC,BD交于O点,由题意可知,OE为△AA1C的中位线,由线面平行的判定定理可证OE∥平面A1C1C;
(2)可补全长方体ABCD-A'B'C'D',利用长方体的体积减去四个三棱锥(以A为顶点,A′A1D1等为底面)的体积即可得答案;
(3)CD⊥平面ADD1,可知CD⊥AD1,若AD1⊥DB1,AD1⊥平面CDD1B1,从而有AD1⊥DD1,取AD中点M,在RtADD1中,2D1M=AD,即可得到a=2b.
(2)可补全长方体ABCD-A'B'C'D',利用长方体的体积减去四个三棱锥(以A为顶点,A′A1D1等为底面)的体积即可得答案;
(3)CD⊥平面ADD1,可知CD⊥AD1,若AD1⊥DB1,AD1⊥平面CDD1B1,从而有AD1⊥DD1,取AD中点M,在RtADD1中,2D1M=AD,即可得到a=2b.
解答: 证明:(1)连接AC,BD交于O点,
证明:(1)连接AC,BD交于O点,
∵E为AA1的中点,O为AC的中点,
∴在△AA1C中,OE为△AA1C的中位线,
∴OE∥A1C,
∵OE?平面A1C1C,A1C?平面A1C1C,
∴OE∥平面A1C1C;
(2)多面体表面共包括10个面,补全长方体ABCD-A'B'C'D',则知多面体ABCD-A1B1C1D1体积为:
VABCD-A1B1C1D1=VABCD-A′B′C′D′-4VA-A′A1D1
=4×4×2-4×
×
×2×2×2
=
,
(3)易知CD⊥平面ADD1,D1B1∥DC,D1B1,OC确定平面CDD1B1,
∵AD1?平面ADD1,
∴CD⊥AD1,若AD1⊥DB1,
∵DB1∩CD=D,
∴AD1⊥平面CDD1B1,
∵DD1?平面CDD1B1,
∴AD1⊥DD1,取AD中点M,
则D1M∥A'A,且D1M=A'A,
∴在RtADD1中,2D1M=AD,即a=2b
即:当a=2b时,AD1⊥DB1.
 证明:(1)连接AC,BD交于O点,
证明:(1)连接AC,BD交于O点,∵E为AA1的中点,O为AC的中点,
∴在△AA1C中,OE为△AA1C的中位线,
∴OE∥A1C,
∵OE?平面A1C1C,A1C?平面A1C1C,
∴OE∥平面A1C1C;
(2)多面体表面共包括10个面,补全长方体ABCD-A'B'C'D',则知多面体ABCD-A1B1C1D1体积为:
VABCD-A1B1C1D1=VABCD-A′B′C′D′-4VA-A′A1D1
=4×4×2-4×
| 1 |
| 3 |
| 1 |
| 2 |
=
| 80 |
| 3 |
(3)易知CD⊥平面ADD1,D1B1∥DC,D1B1,OC确定平面CDD1B1,
∵AD1?平面ADD1,
∴CD⊥AD1,若AD1⊥DB1,
∵DB1∩CD=D,
∴AD1⊥平面CDD1B1,
∵DD1?平面CDD1B1,
∴AD1⊥DD1,取AD中点M,
则D1M∥A'A,且D1M=A'A,
∴在RtADD1中,2D1M=AD,即a=2b
即:当a=2b时,AD1⊥DB1.
点评:本题考查直线与平面平行的判定,考查组合几何体的体积问题,补全长方体是解决问题(2)(3)的关键,考查学生分析问题、转化问题与解决问题的能力,属于难题.

练习册系列答案
相关题目
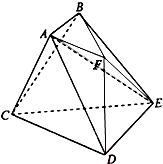 如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且
如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且 如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.
如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.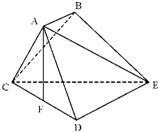 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.