题目内容
(理)已知二次函数f(x)=ax2+bx+c,满足f(0)=f(1)=0,且f(x)的最小值是-![]() .
.
(Ⅰ)求f(x)的解析式;
(Ⅱ)设直线![]() ,若直线l与f(x)的图象以及y轴所围成封闭图形的面积是S1(t),直线l与f(x)的图象所围成封闭图形的面积是S2(t),设
,若直线l与f(x)的图象以及y轴所围成封闭图形的面积是S1(t),直线l与f(x)的图象所围成封闭图形的面积是S2(t),设![]() ,当g(t)取最小值时,求t的值.
,当g(t)取最小值时,求t的值.
(Ⅲ)已知m≥0,n≥0,求证:![]() .
.
答案:
解析:
解析:
|
解:(1)由二次函数图象的对称性,可设 故 (2)据题意,直线 = = 而 令 当 故当 (3) ①+②得: 又 由均值不等式和③知: 故 |

练习册系列答案
相关题目
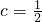 时,求出不等式f(x)<0的解;
时,求出不等式f(x)<0的解;