题目内容
(理)已知二次函数f(x)=ax2+bx+c,(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,f(-2)=0,且当x∈(1,3)时,有f(x)≤
(x+2)2成立.
(1)求f(x)的表达式.
(2)g(x)=4f′(x)-sinx-2数列{an}满足:an+1=g(an),0<a1<1,n=1,2,3,证明:(Ⅰ)0<an+1<an<1;(Ⅱ)an+1<
an3.
| 1 |
| 8 |
(1)求f(x)的表达式.
(2)g(x)=4f′(x)-sinx-2数列{an}满足:an+1=g(an),0<a1<1,n=1,2,3,证明:(Ⅰ)0<an+1<an<1;(Ⅱ)an+1<
| 1 |
| 6 |
分析:(1)根据任意实数x,都有f(x)≥x,知f(2)≥2成立,当x∈(1,3)时,有f(x)≤
(x+2)2成立,取x=2时,f(2)≤2成立,从而f(2)=2,再利用f(-2)=0,即可求得b的值.利用函数f(x)≥x恒成立,通过判别式推出a的值,即可求出函数的解析式.
(2)(Ⅰ)利用数学归纳法证明0<an<1,通过函数的导数证明0<an+1<an<1即可.
(Ⅱ)通过函数的导数判断函数的单调性,然后证明所证不等式即可.
| 1 |
| 8 |
(2)(Ⅰ)利用数学归纳法证明0<an<1,通过函数的导数证明0<an+1<an<1即可.
(Ⅱ)通过函数的导数判断函数的单调性,然后证明所证不等式即可.
解答:解:(1)由条件对任意实数x,都有f(x)≥x,知f(2)≥2成立
∵当x∈(1,3)时,有f(x)≤
(x+2)2成立,
∴取x=2时,f(2)≤
(2+2)2=2成立,
∴f(2)=2.
∴4a+2b+c=2①
∵f(-2)=0
∴4a-2b+c=0②
由①②可得,∴4a+c=2b=1,
∴b=
,c=1-4a,又f(x)≥x恒成立,即ax2+(b-1)x+c≥0恒成立,
∴a>0,△=(
-1)2-4a(1-4a)≤0
可得a=
,∵c=1-4a,
∴c=
,
∴a=
,b=
,c=
,
∴f(x)=
x2+
x+
.
(2):(Ⅰ)证明:0<an<1,
①当n=1时,0<a1<1,成立;
②假设n=k时,0<ak<1,
那么,ak+1=ak-sinak
∵0<ak<1,∴ak-sinak∈(0,1).即ak+1∈(0,1);
由①②可知,0<an<1,n=1,2,3,…成立.
下面证明an>an+1
g(x)=4f′(x)-sinx-2=x-sinx,
g′(x)=1-cosx>0,∴g(x)是增函数,
g(x)≥g(0)=0.
当x∈[0,1)时,sinan>0,an+1=an-sinan,
∴an>an+1
∴0<an+1<an<1;
(Ⅱ)设h(x)=x-sinx-
x3,易证h(x)=x-sinx-
x3
在x∈[0,1)时单调递减,
所以,h(x)<h(0)=0,
∴x-sinx<
x3,an∈(0,1),
∴an+1<
an3.
∵当x∈(1,3)时,有f(x)≤
| 1 |
| 8 |
∴取x=2时,f(2)≤
| 1 |
| 8 |
∴f(2)=2.
∴4a+2b+c=2①
∵f(-2)=0
∴4a-2b+c=0②
由①②可得,∴4a+c=2b=1,
∴b=
| 1 |
| 2 |
∴a>0,△=(
| 1 |
| 2 |
可得a=
| 1 |
| 8 |
∴c=
| 1 |
| 2 |
∴a=
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)=
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
(2):(Ⅰ)证明:0<an<1,
①当n=1时,0<a1<1,成立;
②假设n=k时,0<ak<1,
那么,ak+1=ak-sinak
∵0<ak<1,∴ak-sinak∈(0,1).即ak+1∈(0,1);
由①②可知,0<an<1,n=1,2,3,…成立.
下面证明an>an+1
g(x)=4f′(x)-sinx-2=x-sinx,
g′(x)=1-cosx>0,∴g(x)是增函数,
g(x)≥g(0)=0.
当x∈[0,1)时,sinan>0,an+1=an-sinan,
∴an>an+1
∴0<an+1<an<1;
(Ⅱ)设h(x)=x-sinx-
| 1 |
| 6 |
| 1 |
| 6 |
在x∈[0,1)时单调递减,
所以,h(x)<h(0)=0,
∴x-sinx<
| 1 |
| 6 |
∴an+1<
| 1 |
| 6 |
点评:本题重点考查二次函数的解析式,考查赋值思想,对分析转化的推理能力要求较高,考查数学归纳法以及函数的导数判断函数的单调性的方法.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
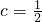 时,求出不等式f(x)<0的解;
时,求出不等式f(x)<0的解;