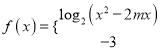题目内容
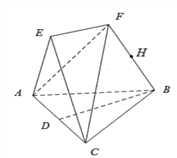
【题目】如图,在三棱锥![]() 与三棱锥
与三棱锥![]() 中,
中,![]() 和
和![]() 都是边长为2的等边三角形,
都是边长为2的等边三角形,![]() 分别为
分别为![]() 的中点,
的中点,![]() ,
,![]() .
.
(Ⅰ)试在平面![]() 内作一条直线
内作一条直线![]() ,当
,当![]() 时,均有
时,均有![]() 平面
平面![]() (作出直线
(作出直线![]() 并证明);
并证明);
(Ⅱ)求两棱锥体积之和的最大值.
【答案】(1)见解析;(2)![]() .
.
【解析】分析:(Ⅰ)即过H点作一平面与平面ABC平行,与平面EFC的交线为直线![]() 。H为中点,所以取
。H为中点,所以取![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,连
,连![]() ,则
,则![]() 即为所作直线
即为所作直线![]() .
.
(Ⅱ)把两个三棱锥的体积和转化为两个四棱锥的体积和,
即![]() ,求梯形EFBD的面积最大值。
,求梯形EFBD的面积最大值。
详解:(Ⅰ)设![]() 的中点为
的中点为![]() ,
,![]() 的中点为
的中点为![]() ,连
,连![]() ,则
,则![]() 即为所作直线
即为所作直线![]() .
.
因为![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 分别为
分别为![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() ,所以
,所以![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
由![]() 知
知![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)因![]() ,所以
,所以![]() 与
与![]() 确定一个平面.
确定一个平面.
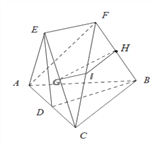
连![]() ,因
,因![]() ,
,![]() 为
为![]() 的中点,
的中点,
所以![]() ,同理
,同理![]() ;
;
又![]() ,所以
,所以![]() 平面
平面![]()
所以![]()
![]()
![]()
其中,![]() ,
,![]() 为梯形
为梯形![]() 的高,
的高,![]() ,
,
当平面![]() 平面
平面![]() 时,
时,![]() ,
,
所以![]()
![]() .
.

练习册系列答案
相关题目