题目内容
【题目】①
；②
；③
（
为常数）这
个条件中选择
个条件，补全下列试题后完成解答，设等差数列
的前
项和为
，若数列的各项均为正整数，且满足公差
，____________.
（1）求数列的通项公式；
（2）令
，求数列
的前项的和.
【答案】条件选择见解析；（1）
；（2）
.
【解析】
（1）选①，根据条件
得出
，由
且
，
，可求得
和
的值，进而可求得等差数列
的通项公式；
选②，由
得出
，由且，，可求得和的值，进而可求得等差数列的通项公式；
选③，由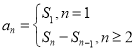
可求得数列的通项公式，求得数列的公差，由该数列为等差数列求得
的值，进而可得出数列的通项公式；
（2）求得
，然后利用分组求和法可求得数列
的前
项和.
（1）由等差数列各项均为正整数，且公差
，知
，.
选①，由
得，由，，得
，
，
；
选②，由
得，由，，得，，；
选③，由
得
，
，则
，且
，
又
，且数列是等差数列，则
，得
，
；
（2）由（1）知，
，
，
所以的前项的和为.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】低密度脂蛋白是一种运载胆固醇进入外周组织细胞的脂蛋白颗粒，可被氧化成氧化低密度脂蛋白，当低密度脂蛋白，尤其是氧化修饰的低密度脂蛋白过量时，它携带的胆固醇便积存在动脉壁上，久了容易引起动脉硬化，因此低密度脂蛋白被称为“坏的胆固醇”.为了调查某地中年人的低密度脂蛋白浓度是否与肥胖有关，随机调查该地100名中年人，得到2×2列联表如下：
肥胖 | 不肥胖 | 总计 | |
低密度脂蛋白不高于 | 12 | 63 | 75 |
低密度脂蛋白高于 | 8 | 17 | 25 |
总计 | 20 | 80 | 100 |
由此得出的正确结论是（ ）
A.有10%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖有关”
B.有10%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖无关”
C.有90%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖有关”
D.有90%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖无关”
