题目内容
8.已知f(x)是定义在R上的偶函数,且x≥0时,f(x)=log${\;}_{\frac{1}{2}}$(x+1).(1)求f(0),f(-1)的值;
(2)求函数f(x)的解析式.
分析 (1)根据f(x)是定义在R上的偶函数,且x≥0时,f(x)=log${\;}_{\frac{1}{2}}$(x+1)代值即可求解;
(2)设x<0,则-x>0代入已知解析式可求解.
解答 解:(1)∵f(x)是定义在R上的偶函数,且x≥0时,f(x)=log${\;}_{\frac{1}{2}}$(x+1)
∴f(0)=0…(2分)
f(-1)=f(1)=-1…(4分)
(2)令x<0,则-x>0,
f(-x)=log${\;}_{\frac{1}{2}}$(-x+1)=f(x)
∴x<0时,f(x)=log${\;}_{\frac{1}{2}}$(-x+1)…(8分)
∴f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(x+1),x≥0}\\{lo{g}_{\frac{1}{2}}(-x+1),x<0}\end{array}\right.$…(10分)
点评 本题为函数的性质的应用,正确运用函数的奇偶性,单调性是解决问题的关键,属中档题.

练习册系列答案
相关题目
19.已知集合A={x|lg(x-1)<1},B={x|$\frac{x+2}{4-x}$≥0},则A∩B=( )
| A. | {x|-2≤x≤4} | B. | {x|4<x<11} | C. | {x|1<x<4} | D. | {x|-2≤x<4} |
8.下列结论正确的是( )
| A. | 若A=R,B=(0,+∞),则f:x→|x|是集合A到集合B的函数 | |
| B. | 若A={x|0≤x≤4},B={y|0≤y≤3},则f:y=$\frac{2}{3}$x是集合A到集合B的映射 | |
| C. | 函数的图象与y轴至少有1个交点 | |
| D. | 若y=f(x)是奇函数,则其图象一定经过原点 |
6.直线x=1,x=2,y=0与曲线y=$\frac{1}{x(x+1)}$围成图形的面积为( )
| A. | ln2 | B. | ln$\frac{4}{3}$ | C. | ln3 | D. | ln3-ln2 |
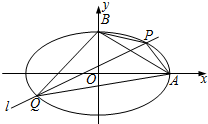 已知平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点和上顶点分别为A,B,椭圆的离心率为$\frac{\sqrt{3}}{2}$,且过点(1,$\frac{\sqrt{3}}{2}$).
已知平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点和上顶点分别为A,B,椭圆的离心率为$\frac{\sqrt{3}}{2}$,且过点(1,$\frac{\sqrt{3}}{2}$).