题目内容
给出下列命题中①向量
 满足
满足 ,则
,则 的夹角为30;
的夹角为30;②
 •
• >0,是
>0,是 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;③将函数y=|x-1|的图象按向量
 =(-1,0)平移,得到的图象对应的函数表达式为y=|x|;
=(-1,0)平移,得到的图象对应的函数表达式为y=|x|;④若(
 +
+ )•(
)•( -
- )=0,则△ABC为等腰三角形;
)=0,则△ABC为等腰三角形;以上命题正确的是 (注:把你认为正确的命题的序号都填上)
【答案】分析:通过举特例判断出①②错;将向量平移转化为图象平移,据解析式与平移的关系判断出③对;通过向量满足的运算律得到④对.
解答:解:利用向量的有关概念,逐个进行判断切入,对于①取特值零向量错误,若前提为非零向量由向量加减法的
平行四边形法则与夹角的概念正确;
对②取特值夹角为0时命题成立,命题应为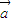 •
•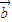 >0是
>0是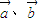 的夹角为锐角的必要条件;
的夹角为锐角的必要条件;
对于③,注意按向量平移的意义,就是图象向左移1个单位,结论正确;
对于④;向量的数量积满足分配律运算,结论正确;
故答案为:③④
点评:本题考查向量的运算法则、向量的数量积公式、向量的运算律、图象平移.注意特殊的向量的应用.
解答:解:利用向量的有关概念,逐个进行判断切入,对于①取特值零向量错误,若前提为非零向量由向量加减法的
平行四边形法则与夹角的概念正确;
对②取特值夹角为0时命题成立,命题应为
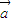 •
•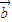 >0是
>0是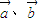 的夹角为锐角的必要条件;
的夹角为锐角的必要条件;对于③,注意按向量平移的意义,就是图象向左移1个单位,结论正确;
对于④;向量的数量积满足分配律运算,结论正确;
故答案为:③④
点评:本题考查向量的运算法则、向量的数量积公式、向量的运算律、图象平移.注意特殊的向量的应用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目