题目内容
给出下列命题中
①向量
，
足|
|=|
|=|
-
|，则
与|
+
|角为30°；
②
•
＞0，是
、
夹角为锐角的充要条件；
③将y=|x-1|的图象按向量
=（-1，0）平移，得到的图象对应的函数表达式为y=|x|；
④若
•
+
=0，△ABC直角三角形．
以上命题正确的是
①向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
②
| a |
| b |
| a |
| b |
③将y=|x-1|的图象按向量
| a |
④若
| AB |
| BC |
| AB2 |
以上命题正确的是
①③④
①③④
（注：把你认为正确的命题的序号都填上）分析：①根据向量加法的平行四边形法则，结合图形判断即可；
②根据方向相同的向量的夹角为0°，利用向量数量积公式判断②是否正确；
③利用图形平移变化规律判断③是否正确；
④根据向量数量积公式及向量的射影，来判断④是否正确．
②根据方向相同的向量的夹角为0°，利用向量数量积公式判断②是否正确；
③利用图形平移变化规律判断③是否正确；
④根据向量数量积公式及向量的射影，来判断④是否正确．
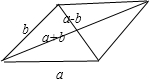
解答：解：①∵向量
，
足|
|=|
|=|
-
|，根据向量加法与减法的法则如图，四边形为内角为60°的菱形．∴①正确；
②∵向量的夹角为0°时，
•
=|
||
|＞0，∴②错误；
③将y=|x-1|的图象按向量
=（-1，0）平移，得函数y=|（x+1）-1|的图象，∴③正确；
④
•
+
2=|
|×（|
|cos（π-∠ABC）+|
|）=0⇒|
|=|
cos∠ABC，∴∠A=90°，故④正确．
故答案是①③④|
| a |
| b |
| a |
| b |
| a |
| b |
②∵向量的夹角为0°时，
| a |
| b |
| a |
| b |
③将y=|x-1|的图象按向量
| a |
④
| AB |
| BC |
| AB |
| AB |
| BC |
| AB |
| AB |
| BC |
故答案是①③④|
点评：本题借助考查命题的真假判断，考查向量的加法、减法法则及向量的数量积．
练习册系列答案
阅读快车系列答案
相关题目
满足
，则
的夹角为
；
＞0，是
的图象按向量
；
，则
为等腰三角形；以上命题正确的是 （注：把你认为正确的命题的序号都填上）
满足
，则
的夹角为30；
•
＞0，是
的夹角为锐角的充要条件；
=（-1，0）平移，得到的图象对应的函数表达式为y=|x|；
+
）•（
-
）=0，则△ABC为等腰三角形；