题目内容
已知平面直角坐标系xOy上的区域D由不等式组
给定,若M(x,y)为D上的动点,点A的坐标为(
,1),则z=
•
的最大值为
|
| 2 |
| OM |
| OA |
4
4
.分析:首先画出可行域,z=
•
代入坐标变为z=
x+y,即y=-
x+z,z表示斜率为 -
的直线在y轴上的截距,故求z的最大值,即求y=-
x+z与可行域有公共点时在y轴上的截距的最大值.
| OM |
| OA |
| 2 |
| 2 |
| 2 |
| 2 |
解答: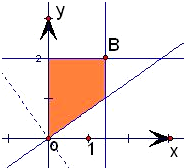 解:由不等式组
解:由不等式组
给定的区域D如图所示:
z=
•
=
x+y,即y=-
x+z
首先做出直线l0:y=-
x,将l0平行移动,当经过B点时在y轴上的截距最大,从而z最大.
因为B(
,2),故z的最大值为4.
故答案为:4.
 解:由不等式组
解:由不等式组
|
z=
| OM |
| OA |
| 2 |
| 2 |
首先做出直线l0:y=-
| 2 |
因为B(
| 2 |
故答案为:4.
点评:本题考查线性规划、向量的坐标表示、平面向量数量积的运算等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.

练习册系列答案
相关题目
 已知平面直角坐标系xOy上的区域D由不等式组
已知平面直角坐标系xOy上的区域D由不等式组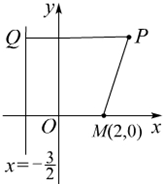 已知平面直角坐标系xOy上的定点M(2,0)和定直线l:x=
已知平面直角坐标系xOy上的定点M(2,0)和定直线l:x=