题目内容
（2013•宜宾二模）已知平面直角坐标系xoy上的区域D由不等式组
给定，若M（x，y）为D上的动点，A的坐标为（-1，1），则
•
的取值范围是
|
| OA |
| OM |
[0，2]
[0，2]
．分析：作出题中不等式组对应的平面区域如图，根据向量数量积的坐标运算公式可得z=-x+y，再进行直线平移法可得z的最值，从而得出
•
的取值范围．
| OA |
| OM |
解答：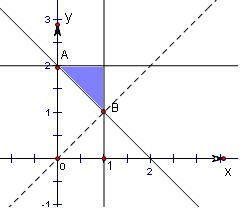
解：作出可行域如右图
∵M（x，y），A（0，2），B（1，1）
∴z=
•
=-x+y，
将直线l：z=-x+y进行平移，当它经过交点A（0，2）时，z达到最大值2，当它经过交点B（1，1）时，z达到最小值，
则z=-x+y的取值范围是[0，2]．
∴则
•
的取值范围是[0，2]．
故答案为：[0，2]．
解：作出可行域如右图∵M（x，y），A（0，2），B（1，1）
∴z=
| OA |
| OM |
将直线l：z=-x+y进行平移，当它经过交点A（0，2）时，z达到最大值2，当它经过交点B（1，1）时，z达到最小值，
则z=-x+y的取值范围是[0，2]．
∴则
| OA |
| OM |
故答案为：[0，2]．
点评：本题以向量数量积的坐标运算为载体，考查了简单的线性规划的知识，属于基础题．采用直线平移法，是解决此类问题的关键所在．
练习册系列答案
相关题目
（2013•宜宾二模）函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜
（2013•宜宾二模）在一个几何体的三视图中，正视图和俯视图如图所示，则该几何体的体积为（ ）
（2013•宜宾二模）如果执行如图所示的框图，输入N=10，则输出的数等于（ ）