Question

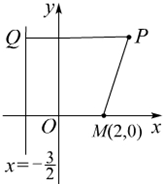已知平面直角坐标系xOy上的定点M（2，0）和定直线l：x=-

3

2

，动点P在直线l上的射影为Q，且4(

PQ

+

PM

)•(

PQ

-

PM

)+2

PM

•

OM

=1．
（1）求点P的轨迹C的方程；
（2）设A、B是轨迹C上两个动点，

MA

=λ

MB

，λ∈R，∠AOB=θ，请把△AOB的面积S表示为θ的函数，并求此函数的定义域．

Answer 1

分析：（1）设P（x，y），根据4(

PQ

+

PM

)•(

PQ

-

PM

)+2

PM

•

OM

=1，可得4

PQ

2-4

PM

2-4(x-2)=1
即4(x+

3

2

)2-4[(x-2)2+y2]-4(x-2)=1，化简可得y²=6x；
（2）由

FA

=λ

FB

知A、B、M共线，设AB的方程为x=my+2，与抛物线方程联立消去x得y²-6my-12=0，从而可得△AOB的面积S表示为θ的函数，利用S=

1

2

|OM||y1-y2|=|y1-y2|≥2

|y1y2|

=4

3

，可确定函数的定义域．

解答：解：（1）设P（x，y）
∵4(

PQ

+

PM

)•(

PQ

-

PM

)+2

PM

•

OM

=1．
∴4

PQ

2-4

PM

2-4(x-2)=1
∴4(x+

3

2

)2-4[(x-2)2+y2]-4(x-2)=1
整理得y²=6x；
（2）由

FA

=λ

FB

知A、B、M共线，设AB的方程为x=my+2，
与抛物线方程联立消去x得y²-6my-12=0，
y₁y₂=-12，x₁x₂=

(y1y2)2

36

=4，

OA

•

OB

=-8．
S=

1

2

|

OA

||

OB

|sinθ=

1

2

×

OA

•

OB

tanθ=-4tanθ．
因为S=

1

2

|OM||y1-y2|=|y1-y2|≥2

|y1y2|

=4

3

，
所以-4tanθ≥4

3

，
即tanθ≤-

3

，解得

π

2

＜θ＜

2π

3

．

点评：本题以向量条件为载体，考查抛物线的方程，考查三角形面积的计算，正确转化是解题的关键．