题目内容
12.已知函数f(x)=$\sqrt{ax-1}$在[1,3]上是增函数,求a的取值范围.分析 设g(t)=at-1,根据复合函数单调性之间的关系进行求解即可.
解答 解:设g(t)=at-1,则函数y=$\sqrt{t}$为增函数,
∴若f(x)=$\sqrt{ax-1}$在[1,3]上是增函数,
则等价为g(x)=ax-1,在[1,3]上是增函数且g(1)≥0,
即a>0且g(1)=a-1≥0,
即a>0且a≥1,
故a≥1.
点评 本题主要考查函数单调性的应用,根据复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
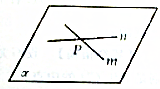 如图,直线m、n在平面α内,且m与n相交于点P,试用符号语言写出所有点与线、点与面、线与线、线与面之间的关系.
如图,直线m、n在平面α内,且m与n相交于点P,试用符号语言写出所有点与线、点与面、线与线、线与面之间的关系.