题目内容
(本小题满分12分)已知⊙C:x2+y2-2x-2y+1=0,直线l与⊙C相切且分别交x轴、y轴正向于A、B两点,O为坐标原点,且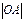 =a,
=a,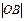 =b(a>2,b>2).
=b(a>2,b>2).
(Ⅰ)求线段AB中点的轨迹方程.
(Ⅱ)求△ABC面积的极小值.
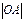 =a,
=a,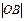 =b(a>2,b>2).
=b(a>2,b>2).(Ⅰ)求线段AB中点的轨迹方程.
(Ⅱ)求△ABC面积的极小值.
解:C:(x-1)2+(y-1)2=1,A(a,O),B(O,b) .设直线AB的方程为
bx+ay-ab=0,∵直线AB与⊙C相切,
∴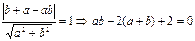 ①…………………………………2分
①…………………………………2分
(Ⅰ)设AB中点P(x,y),则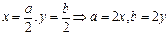 代入
代入 ①得P点的轨迹方程:2xy
①得P点的轨迹方程:2xy
-2x-2y+1=0,∵a>2,∴x> 1.
1.
∴P点的轨迹方程为(x-1)(y-1)= (x>1).
(x>1). …………………………………7分
…………………………………7分
(Ⅱ)由①得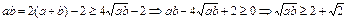 ,当且仅当
,当且仅当
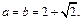 时等号成立.
时等号成立.
S△AOB= ab≥3+2
ab≥3+2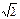 .………………………………12分
.………………………………12分
bx+ay-ab=0,∵直线AB与⊙C相切,
∴
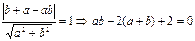 ①…………………………………2分
①…………………………………2分(Ⅰ)设AB中点P(x,y),则
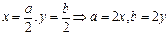 代入
代入 ①得P点的轨迹方程:2xy
①得P点的轨迹方程:2xy-2x-2y+1=0,∵a>2,∴x>
 1.
1.∴P点的轨迹方程为(x-1)(y-1)=
 (x>1).
(x>1). …………………………………7分
…………………………………7分(Ⅱ)由①得
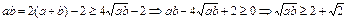 ,当且仅当
,当且仅当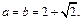 时等号成立.
时等号成立.S△AOB=
 ab≥3+2
ab≥3+2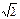 .………………………………12分
.………………………………12分略

练习册系列答案
相关题目
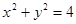
 所围成的较小图形的面积( )
所围成的较小图形的面积( )


 N(1,0)的距离的比为。
N(1,0)的距离的比为。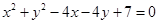 上一点,且点P到直线
上一点,且点P到直线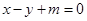 距离的最小值为
距离的最小值为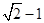 ,则m的值为 ( )
,则m的值为 ( )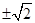
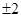
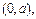 其斜率为1,且与圆
其斜率为1,且与圆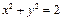 相切,则
相切,则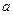 的值为( )
的值为( )




 与直线
与直线 相切,则
相切,则 ( )
( )


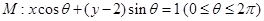 ,则下列命题中是真命题的个数是
,则下列命题中是真命题的个数是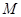 中所有直线均经过一个定点 ⑤存在定点
中所有直线均经过一个定点 ⑤存在定点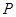 不在
不在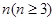 ,存在正
,存在正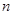 边形,其所有边均在
边形,其所有边均在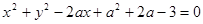 表示圆,且过点
表示圆,且过点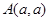 可作该圆的两条切线,则实数
可作该圆的两条切线,则实数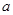 的取值范围为 .
的取值范围为 . 和圆
和圆 交于
交于 两点,且
两点,且 ,则
,则  ____▲___。
____▲___。