题目内容
【题目】设抛物线的顶点为A,焦点为F.过F作直线l与抛物线交于点P、Q,直线AP、AQ分别与抛物线的准线交于点M、N.问:直线l满足什么条件时,三直线PN、QM、AF恒交于一点?
【答案】见解析
【解析】
当直线![]() 时,由抛物线的对称性可知,四边形PQMN是矩形,此时,三直线PN、QM、AF互相平行.
时,由抛物线的对称性可知,四边形PQMN是矩形,此时,三直线PN、QM、AF互相平行.
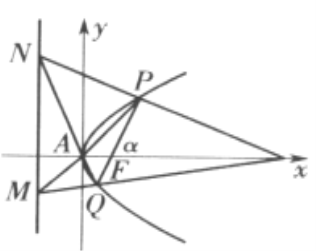
当直线l不与AF垂直时,建立如图的直角坐标系.
设抛物线的方程为![]() ,
,![]()
并设![]() 、
、![]() .
.
由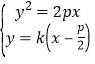 ,得
,得![]() .
.
故![]() ,
,![]() .
.
因为![]() ,所以,
,所以,![]() ,
,![]() .
.
由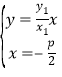 及
及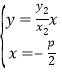 分别得
分别得![]() ,
,![]() .
.
故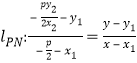 ,
,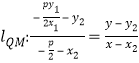
令y=0,则![]()
![]()
故PN、QM与AF的交点分别为![]() 、
、![]() .
.
于是,三直线PN、QM、AF交于一点![]() 点S和T重合
点S和T重合
![]() .
.
化简得![]()
将![]() ,
,![]() 代入上式得
代入上式得![]()
即![]() .
.
因为![]() ,所以,上式成立.
,所以,上式成立.
此时,三直线PN、QM、AF恒交于一点.
综上所述,当直线l不与AF垂直时,三直线PN、QM、AF交于一点.

练习册系列答案
相关题目