题目内容
7．已知椭圆$\frac{x^2}{25}$+$\frac{y^2}{9}$=1的两个焦点为F1，F2，P为椭圆上一点，∠F1PF2=θ（1）求椭圆的长轴长，短轴长，顶点，离心率．
（2）求证：$S_{△{F_1}P{F_2}}$=9tan$\frac{θ}{2}$．
分析 （1）由椭圆的标准方程可以求出椭圆的长轴长，短轴长，顶点，离心率
（2）由椭圆的定义可得|PF1|+|PF2|=2a，再由余弦定理可得|PF1|2+|PF2|2-|F1F2|2=2|PF1||PF2|cosθ，从而可得|PF1||PF2|=$\frac{2{b}^{2}}{1+cosθ}$，从而求△F1PF2的面积．
解答 解：（1）由椭圆$\frac{x^2}{25}$+$\frac{y^2}{9}$=1，可得a2=25，b2=9，c2=a2-b2=25-9=16，即a=5，b=3，c=4，
则长轴长为2a=10，短轴长2b=6，顶点分别为（5，0），（-5，0），（0，3），（0，-3），
e=$\frac{c}{a}$=$\frac{4}{5}$
（2）由题意，|PF1|+|PF2|=2a=10，
又∵|PF1|2+|PF2|2-|F1F2|2=2|PF1||PF2|cosθ，
∴（|PF1|+|PF2|）2-|F1F2|2=2|PF1||PF2|+2|PF1||PF2|cosθ，
∴4a2-4c2=2|PF1||PF2|（1+cosθ）=4b2=36，
∴|PF1||PF2|=$\frac{18}{1+coθ}$，
∴S△F1PF2=$\frac{1}{2}$|PF1||PF2|•sinθ=9•$\frac{sinθ}{1+cosθ}$=9tan$\frac{θ}{2}$．
点评 本题考查了椭圆的定义及余弦定理的应用，属于中档题
练习册系列答案
相关题目
3．“${log_a}^x={log_a}^y$（a＞0且a≠1）”是“x=y”的（ ）
| A． | 充要条件 | B． | 充分不必要条件 | ||
| C． | 必要不充分条件 | D． | 既不充分也不必要条件 |
20．若全集U={x|x≤5，x∈N*}，集合A={1，3，4}，B={2，4}，则（∁UA）∪B为（ ）
| A． | {2，4，5} | B． | {1，3，4} | C． | {1，2，4} | D． | {2，3，4，5} |
19．已知f（x）=log2$\frac{x+1}{x-1}$（其中x＞1），g（x）=x2-2ax+a2+b（其中x∈R，a＞0，b＞1），则下列判断正确的是（ ）
| A． | f（g（a-1））＞f（g（a）） | B． | f（g（$\frac{2a}{3}$））＞f（g（$\frac{5a}{3}$）） | ||
| C． | g（f（$\frac{{4}^{n}+1}{{4}^{n}-1}$））＞g（f（3））（其中a≠0且a$≠\frac{1}{2}$） | D． | g（f（$\frac{{2}^{n}+1}{{2}^{n}-1}$））＞g（f（3））（其中a≠0，且a≠1） |
16．
2014 年12 月28 日开始，北京市公共电汽车和地铁按照里程分段计价．具体如下表．（不考虑公交卡折扣情况）
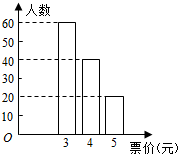
已知在北京地铁四号线上，任意一站到陶然亭站的票价不超过5 元，现从那些只乘坐四号线地铁，且在陶然亭出站的乘客中随机选出120 人，他们乘坐地铁的票价统计如图所示．
（Ⅰ）如果从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中任选1 人，试估计此人乘坐地铁的票价小于5 元的概率；
（Ⅱ）从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中随机选2 人，记x 为这2人乘坐地铁的票价和，根据统计图，并以频率作为概率，求X 的分布列和数学期望；
（Ⅲ）小李乘坐地铁从A 地到陶然亭的票价是5 元，返程时，小李乘坐某路公共电汽车所花交通费也是5 元，假设小李往返过程中乘坐地铁和公共电汽车的路程均为s 公里，试写出s 的取值范围．（只需写出结论）
2014 年12 月28 日开始，北京市公共电汽车和地铁按照里程分段计价．具体如下表．（不考虑公交卡折扣情况）| 乘公共汽车方案 | 10公里（含）内2元； 10公里以上部分，每增加1元可乘坐5公里（含） |
| 乘坐地铁方案（不含机场线） | 6公里（含）内3元 6公里至12公里（含）4元 12公里至22公里（含）5元 |
| 22公里至32公里（含）6元 32公里以上部分，每增加1元可乘坐20公里（含） |
（Ⅰ）如果从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中任选1 人，试估计此人乘坐地铁的票价小于5 元的概率；
（Ⅱ）从那些只乘坐四号线地铁，且在陶然亭站出站的乘客中随机选2 人，记x 为这2人乘坐地铁的票价和，根据统计图，并以频率作为概率，求X 的分布列和数学期望；
（Ⅲ）小李乘坐地铁从A 地到陶然亭的票价是5 元，返程时，小李乘坐某路公共电汽车所花交通费也是5 元，假设小李往返过程中乘坐地铁和公共电汽车的路程均为s 公里，试写出s 的取值范围．（只需写出结论）