题目内容
【题目】已知函数![]() .
.
(1)设![]() ,将函数
,将函数![]() 表示为关于
表示为关于![]() 的函数
的函数![]() ,求
,求![]() 的解析式;
的解析式;
(2)对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】试题分析 :(1)首先由两角和的正弦公式可得![]() ,进而即可求出
,进而即可求出![]() 的取值范围;接下来对已知的函数利用
的取值范围;接下来对已知的函数利用![]() 进行表示;
进行表示;
对于(2),首先由![]() 的取值范围,求出
的取值范围,求出![]() 的取值范围,再对已知进行恒等变形可得
的取值范围,再对已知进行恒等变形可得![]() 在区间
在区间![]() 上恒成立,据此即可得到关于
上恒成立,据此即可得到关于![]() 的不等式,解不等式即可求出
的不等式,解不等式即可求出![]() 的取值范围.
的取值范围.
试题解析:
(1)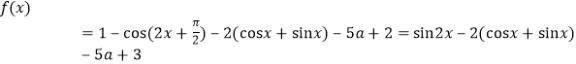 ,
,
因为![]() ,所以
,所以![]() ,其中
,其中![]() ,
,
即![]() ,
,![]() .
.
(2)由(1)知,当![]() 时,
时,![]() ,
,
又![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() ,从而
,从而![]() ,
,
要使不等式![]() 在区间
在区间![]() 上恒成立,只要
上恒成立,只要![]() ,
,
解得:![]() .
.
点晴:本题考查的是求函数的解析式及不等式恒成立问题. (1)首先![]() ,可求出
,可求出![]() 的取值范围;接下来对已知的函数利用
的取值范围;接下来对已知的函数利用![]() 进行表示;(2)先求二次函数
进行表示;(2)先求二次函数![]() ,再解不等式
,再解不等式![]() .
.

练习册系列答案
相关题目