题目内容
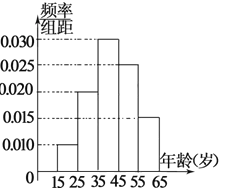
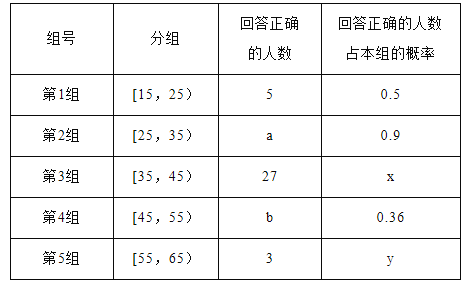
【题目】某市电视台为了宣传,举办问答活动,随机对该市15至65岁的人群进行抽样,频率分布直方图及回答问题统计结果如表所示:
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取3人颁发幸运奖,求:所抽取的人中第3组至少有1人获得幸运奖的概率.
【答案】(1)![]() ;(2)第2,3,4组每组应各依次抽取
;(2)第2,3,4组每组应各依次抽取![]() 人,
人,![]() 人,
人,![]() 人;(3)
人;(3)![]() .
.
【解析】
试题分析:(1)根据第一组的答对的人数和概率,计算得第一组的人数,根据频率可计算的总人数为![]() ,再根据频率分布直方图可计算得
,再根据频率分布直方图可计算得![]() ;(2)三组答对人数比为
;(2)三组答对人数比为![]() ,故分别抽取
,故分别抽取![]() 人;(3)利用列举法求得概率为
人;(3)利用列举法求得概率为![]() .
.
试题解析:
(1)第1组人数![]() ,所以
,所以![]() ,
,
第2组人数![]() ,所以
,所以![]() ,
,
第3组人数![]() ,所以
,所以![]() ,
,
第4组人数![]() ,所以
,所以![]() ,
,
第5组人数![]() ,所以
,所以![]() ,
,
(2)第2,3,4组回答正确的人的比为![]() ,所以第2,3,4组每组应各依次抽取2人,3人,1人.
,所以第2,3,4组每组应各依次抽取2人,3人,1人.
(3)记抽取的6人中,第2组的记为![]() ,第3组的记为
,第3组的记为![]() ,第4组的记为
,第4组的记为![]() ,则从6名学生中任取3名的所有可能的情况有20种,它们是:
,则从6名学生中任取3名的所有可能的情况有20种,它们是:
![]()
![]()
![]() ,
,
其中记“第3组至少有1人”为事件![]() ,则
,则![]() 的对立事件是“第3组的没有选到”,其基本事件个数是1个,即
的对立事件是“第3组的没有选到”,其基本事件个数是1个,即![]() ,故所求概率为
,故所求概率为![]() .
.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目