题目内容
(本小题共13分)已知函数
 .
.
(Ⅰ)若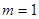 ,求曲线
,求曲线 在点
在点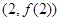 处的切线方程;
处的切线方程;
(Ⅱ)若函数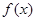 在区间
在区间 上单调递增,求实数
上单调递增,求实数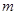 的取值范围.
的取值范围.
【答案】
解:(Ⅰ)当 时,
时,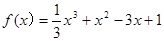 ,
, .
.
 ,
, .
………3分
.
………3分
所以所求切线方程为 即
即 . ……5分
. ……5分
(Ⅱ) .
.
令 ,得
,得 .
………7分
.
………7分
由于 ,
, ,
, 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
+ |
0 |
— |
0 |
+ |
|
|
单调增 |
极大值 |
单调减 |
极小值 |
单调增 |
所以函数 的单调递增区间是
的单调递增区间是 和
和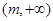 . …………9分
. …………9分
要使 在区间
在区间 上单调递增,
上单调递增,
应有  ≤
≤ 或
或  ≥
≥ ,
,
解得 ≤
≤ 或
或 ≥
≥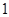 .
…………11分
.
…………11分
又  且
且 ,
…………12分
,
…………12分
所以 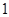 ≤
≤ .
.
即实数 的取值范围
的取值范围  .
…………13分
.
…………13分
【解析】本题考查切线方程和函数的最值问题。考查学生利用导数法解决问题的能力.如果 在点
在点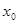 可导,则曲线
可导,则曲线 在点(
在点( )处的切线方程为
)处的切线方程为
 注意:“过点
注意:“过点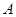 的曲线的切线方程”与“在点
的曲线的切线方程”与“在点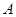 处的切线方程”是不相同的,后者
处的切线方程”是不相同的,后者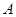 必为切点,前者未必是切点.本题的第一文是在点
必为切点,前者未必是切点.本题的第一文是在点 处,故直接求解即可;通过对函数求导,分析函数的单调性,寻求函数的最值是常规的解题思路,往往和分类讨论思想结合在一起考查。如本题的第二问,通过函数单调递增的等价性判断参数m范围.
处,故直接求解即可;通过对函数求导,分析函数的单调性,寻求函数的最值是常规的解题思路,往往和分类讨论思想结合在一起考查。如本题的第二问,通过函数单调递增的等价性判断参数m范围.

练习册系列答案
相关题目

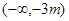

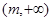

 。
。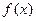 的最小正周期:
的最小正周期: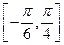 上的最大值和最小值。
上的最大值和最小值。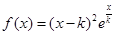 。
。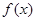 的单调区间;
的单调区间;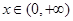 ,都有
,都有 ,求
,求 的取值范围。
的取值范围。 :
: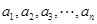 ,其中等于
,其中等于 的项有
的项有 个
个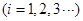 ,
,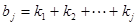
 ,
,
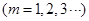 .
. ,求
,求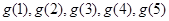 ;
;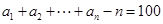 ,求函数
,求函数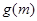 的最小值.
的最小值. ,
,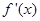 为函数
为函数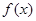 的导函数.
的导函数. 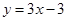 ,求
,求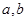 的值;
的值; ,求函数
,求函数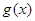 的单调区间.
的单调区间.