题目内容
已知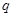 和
和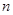 均为给定的大于1的自然数,设集合
均为给定的大于1的自然数,设集合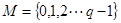 ,集合
,集合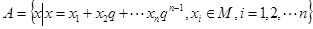 ,
,
(1)当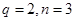 时,用列举法表示集合A;
时,用列举法表示集合A;
(2)设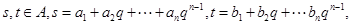 其中
其中 证明:若
证明:若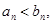 则
则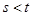 .
.
(1) 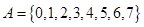 , (2) 详见解析.
, (2) 详见解析.
解析试题分析:(1)本题实质是具体理解新定义,当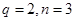 时,
时,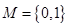 ,
,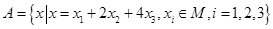 ,再分别对
,再分别对 取
取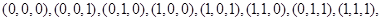 得到
得到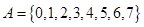 (2)证明大小不等式,一般利用作差法.
(2)证明大小不等式,一般利用作差法.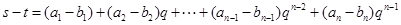 ,根据新定义:
,根据新定义: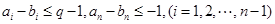 ,所以
,所以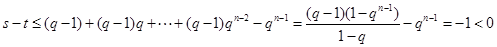 ,即
,即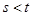 .
.
解:当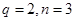 时,
时,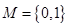 ,
,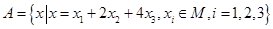 ,可得,
,可得,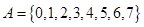
证明:由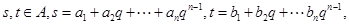
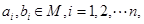 及
及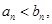 可得
可得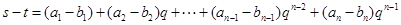
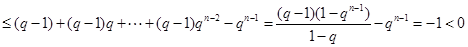
所以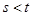 .
.
考点:新定义,作差证明不等式,等比数列求和

练习册系列答案
相关题目
题目内容
已知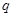 和
和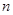 均为给定的大于1的自然数,设集合
均为给定的大于1的自然数,设集合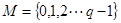 ,集合
,集合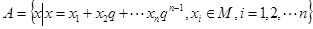 ,
,
(1)当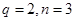 时,用列举法表示集合A;
时,用列举法表示集合A;
(2)设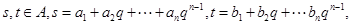 其中
其中 证明:若
证明:若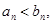 则
则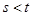 .
.
(1) 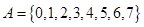 , (2) 详见解析.
, (2) 详见解析.
解析试题分析:(1)本题实质是具体理解新定义,当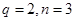 时,
时,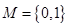 ,
,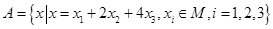 ,再分别对
,再分别对 取
取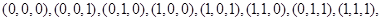 得到
得到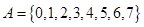 (2)证明大小不等式,一般利用作差法.
(2)证明大小不等式,一般利用作差法.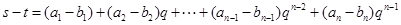 ,根据新定义:
,根据新定义: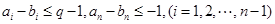 ,所以
,所以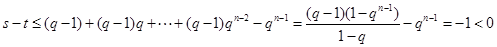 ,即
,即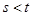 .
.
解:当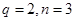 时,
时,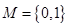 ,
,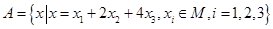 ,可得,
,可得,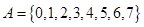
证明:由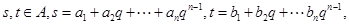
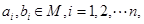 及
及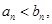 可得
可得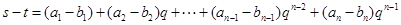
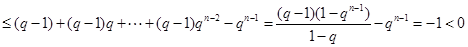
所以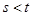 .
.
考点:新定义,作差证明不等式,等比数列求和
