题目内容
点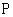 在椭圆
在椭圆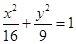 上,求点
上,求点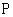 到直线
到直线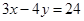 的最大距离和最小距离。
的最大距离和最小距离。
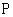 在椭圆
在椭圆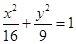 上,求点
上,求点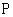 到直线
到直线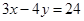 的最大距离和最小距离。
的最大距离和最小距离。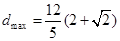 ;
;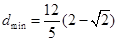 。
。利用点到直线的距离公式可知,设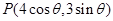 ,则
,则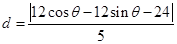
即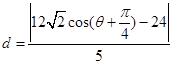 ,当
,当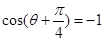 时,
时,
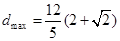 ;
;
当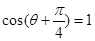 时,
时,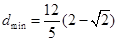 。结论可知。
。结论可知。
解:设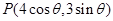 ,则
,则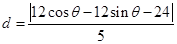
即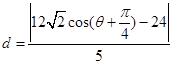 ,当
,当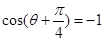 时,
时,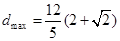 ;
;
当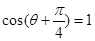 时,
时,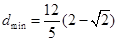 。
。
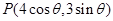 ,则
,则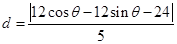
即
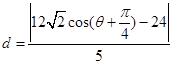 ,当
,当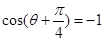 时,
时,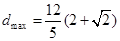 ;
;当
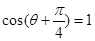 时,
时,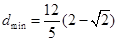 。结论可知。
。结论可知。解:设
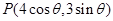 ,则
,则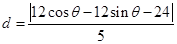
即
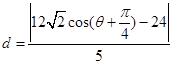 ,当
,当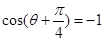 时,
时,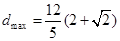 ;
;当
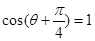 时,
时,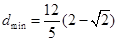 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
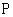 在椭圆
在椭圆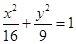 上,求点
上,求点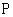 到直线
到直线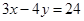 的最大距离和最小距离。
的最大距离和最小距离。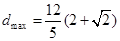 ;
;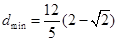 。
。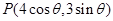 ,则
,则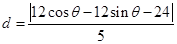
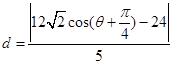 ,当
,当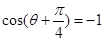 时,
时,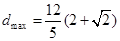 ;
;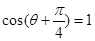 时,
时,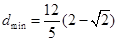 。结论可知。
。结论可知。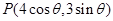 ,则
,则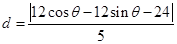
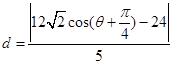 ,当
,当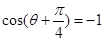 时,
时,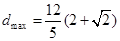 ;
;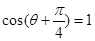 时,
时,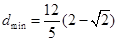 。
。
 阅读快车系列答案
阅读快车系列答案