题目内容
17.函数f(x)=$\frac{\sqrt{x-1}}{1-|x-1|}$的定义域为{x|x≥1且x≠2}.分析 利用分母不为0,开偶次方被开方数非负,列出不等式组求解即可.
解答 解:要使函数有意义,可得:$\left\{\begin{array}{l}x-1≥0\\ 1-|x-1|≠0\end{array}\right.$,解得x≥1且x≠2.
函数f(x)=$\frac{\sqrt{x-1}}{1-|x-1|}$的定义域为:{x|x≥1且x≠2}.
故答案为:{x|x≥1且x≠2}.
点评 本题考查函数的定义域的求法,是基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
12.(ax+$\frac{1}{x}$)(2x-1)5的展开式中各项系数的和为2,则a的值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
9.若直线a∥α,直线b∥α,则a与b( )
| A. | 平行 | B. | 异面 | C. | 平行或异面 | D. | 相交、平行或异面 |
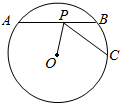 如图,点P为⊙O的弦AB上一点,且AP=9,BP=4,连接OP,作PC⊥OP交圆于C,则PC的长为( )
如图,点P为⊙O的弦AB上一点,且AP=9,BP=4,连接OP,作PC⊥OP交圆于C,则PC的长为( )