题目内容
5.将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题:①△DBC是等边三角形;
②AC⊥BD;
③三棱锥D-ABC的体积是$\frac{{\sqrt{2}}}{6}$.
其中正确命题的序号是( )
| A. | ①③ | B. | ①② | C. | ②③ | D. | ①②③ |
分析 画出图形,根据图可知BD=DO=1,再由BC=$\sqrt{2}$DC=1,判断①的正误.
由AC⊥DO,AC⊥BO,可得AC⊥平面DOB,从而有AC⊥BD,判断②的正误.
求出三棱锥D-ABC的体积,判断③的正误.
解答 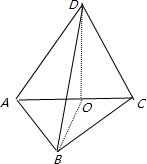 解:如图所示:BD=$\sqrt{2}$DO=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=1,
解:如图所示:BD=$\sqrt{2}$DO=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=1,
又BC=DC=1,
∴面DBC是等边三角形,①正确;
∵AC⊥DO,AC⊥BO,
∴AC⊥平面DOB,
∴AC⊥BD,②正确;
三棱锥D-ABC的体积=$\frac{1}{3}$S△ABC•OD=$\frac{1}{3}$•$\frac{1}{2}$•1•1•$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{12}$,③不正确.
故选:B.
点评 本题主要考查折叠问题,要注意折叠前后的改变的量和位置,不变的量和位置,属中档题.

练习册系列答案
相关题目
6.异面直线l与m所成的角为$\frac{π}{3}$,异面直线l与n所成的角为$\frac{π}{4}$,则异面直线m与n所成角的范围是( )
| A. | [$\frac{π}{6}$,$\frac{π}{2}$] | B. | [$\frac{π}{12}$,$\frac{π}{2}$] | C. | [$\frac{π}{12}$,$\frac{7π}{12}$] | D. | [$\frac{π}{6}$,$\frac{7π}{12}$] |
10. 正四面体ABCD的棱长为2,棱AD与平面α所成的角θ∈[$\frac{π}{3}$,$\frac{π}{2}$],且顶点A在平面α内,B,C,D均在平面α外,则棱BC的中点E到平面α的距离的取值范围是( )
正四面体ABCD的棱长为2,棱AD与平面α所成的角θ∈[$\frac{π}{3}$,$\frac{π}{2}$],且顶点A在平面α内,B,C,D均在平面α外,则棱BC的中点E到平面α的距离的取值范围是( )
 正四面体ABCD的棱长为2,棱AD与平面α所成的角θ∈[$\frac{π}{3}$,$\frac{π}{2}$],且顶点A在平面α内,B,C,D均在平面α外,则棱BC的中点E到平面α的距离的取值范围是( )
正四面体ABCD的棱长为2,棱AD与平面α所成的角θ∈[$\frac{π}{3}$,$\frac{π}{2}$],且顶点A在平面α内,B,C,D均在平面α外,则棱BC的中点E到平面α的距离的取值范围是( )| A. | [$\frac{\sqrt{3}}{2}$,1] | B. | [$\frac{\sqrt{3}-\sqrt{2}}{2}$,1] | C. | [$\frac{\sqrt{3}-\sqrt{2}}{2}$,$\frac{\sqrt{3}+\sqrt{2}}{2}$] | D. | [$\frac{\sqrt{3}-\sqrt{2}}{2}$,$\sqrt{3}$] |
 如图,在四棱椎P-ABCD中,底面ABCD是边长为6的菱形,侧棱PD⊥平面ABCD,BD=6,PD=3$\sqrt{6}$,点E,F分别是PB,CB上靠近点B的一个三等分点.
如图,在四棱椎P-ABCD中,底面ABCD是边长为6的菱形,侧棱PD⊥平面ABCD,BD=6,PD=3$\sqrt{6}$,点E,F分别是PB,CB上靠近点B的一个三等分点. 有大小形状完全相同的4个红球,2个白球,放入如图所示的九个格子中,每个格子至多放入1个小球,相邻格子(即有公共边的两个正方形)中放入的小球不同色,则不同的方法共有( )
有大小形状完全相同的4个红球,2个白球,放入如图所示的九个格子中,每个格子至多放入1个小球,相邻格子(即有公共边的两个正方形)中放入的小球不同色,则不同的方法共有( )