题目内容
17.设f(x)=e•ex,e=2.71828…是自然对数的底.(1)求曲线f(x)在点M(0,e)处的切线方程;
(2)设g(x)=f(x)-kx(k∈R),试探究函数g(x)的单调性;
(3)若f(x)>kx总成立,求k的取值范围.
分析 (1)求出导数,求得切线的斜率,由斜截式方程,即可得到所求;
(2)求出导数,对k讨论,当k≤0时,当k>0时,由导数大于0,求得增区间,由导数小于0,得到减区间;
(3)方法一、求得导数,对k讨论,当k=0,k<0,k>0,f(x)>kx总成立等价于g(x)min>0.解不等式即可得到所求范围;
方法二、先讨论k<0不成立,再由当x∈(0,+∞)时,f(x)>kx总成立,等价于k<$\frac{f(x)}{x}$总成立,
即为$k<\frac{f(x)}{x}$的最小值.求出右边函数的最小值,即可得到所求.
解答 解:(1)f′(x)=e1+x,
∴过M的曲线f(x)的切线的斜率k=f′(0)=e,
∴过M的曲线f(x)的切线方程为y=ex+e.
(2)由条件知g(x)=e•ex-kx,g′(x)=ex+1-k,
当k≤0时,显然g′(x)>0,∴g(x)在R是增函数.
当k>0时,令g′(x)>0得x>lnk-1;令g′(x)<0得x<lnk-1.
∴g(x)的增区间为(lnk-1,+∞),减区间为(-∞,lnk-1);
(3)解法一:当k<0时,由y=f(x)和y=kx的图象知f(x)>kx不可能总成立.
当k=0时,由f(x)>0,kx=0知f(x)>kx总成立.
当k>0时,f(x)>kx总成立等价于g(x)min>0.
由(2)知g(x)min=g(lnk-1)=k(2-lnk)>0,
解得0<k<e2,
综上所述:k的取值范围是[0,e2);
解法二:若k<0,由y=f(x)和y=kx的图象知f(x)>kx不可能总成立,
∴k≥0.
当x∈(-∞,0]时,有f(x)=e1+x>0,kx≤0,
∴f(x)>kx总成立;
当x∈(0,+∞)时,f(x)>kx总成立,等价于k<$\frac{f(x)}{x}$总成立,
∴$k<\frac{f(x)}{x}$的最小值.
记$F(x)=\frac{f(x)}{x},则F'(x)=\frac{f'(x)×x-f(x)}{x^2}=\frac{{x{e^{1+x}}-{e^{1+x}}}}{x^2}=\frac{{(x-1){e^{1+x}}}}{x^2}(x>0)$,
显然x∈(0,1)时,F′(x)<0; x∈(1,+∞)时,F′(x)>0.
∴F(x)的增区间为(1,+∞),减区间为(0,1),
∴$F{(x)_{min}}=F(1)={e^2}$,
∴k<e2综上所述:k的取值范围是[0,e2).
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,考查不等式的恒成立问题,注意运用单调性和参数分离,考查运算能力,属于中档题.

| A. | 0.60 | B. | 0.63 | C. | 0.65 | D. | 0.68 |
| A. | $\frac{150}{7}$min | B. | $\frac{15}{7}$h | C. | 21.5 min | D. | 2.15 h |
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{3\sqrt{10}}{10}$ |
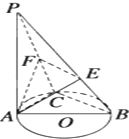 如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是点A在PB、PC上的射影,给出下列结论:
如图,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E、F分别是点A在PB、PC上的射影,给出下列结论: