题目内容
设函数
(Ⅰ)试问函数 能否在
能否在 处取得极值,请说明理由;
处取得极值,请说明理由;
(Ⅱ)若 ,当
,当 时,函数
时,函数 的图像有两个公共点,求
的图像有两个公共点,求 的取值范围.
的取值范围.
(Ⅰ) (Ⅱ)
(Ⅱ)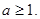
解析试题分析:(Ⅰ)由题设可知: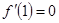 且
且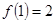 , 即
, 即 ,解得
,解得
(Ⅱ)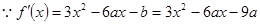 , 又
, 又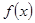 在
在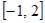 上为减函数,
上为减函数, 
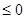 对
对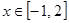 恒成立, 即
恒成立, 即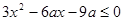 对
对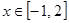 恒成立.
恒成立.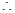
 且
且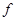
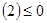 ,
, 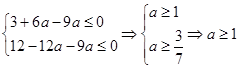 ,
,
 的取值范围是
的取值范围是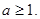
考点:利用导数研究函数的极值,不等式恒成立问题。
点评:中档题,利用导数研究函数的极值,一般遵循“求导数、求驻点、研究导数的正负、确定极值”,利用“表解法”,清晰易懂。不等式恒成立问题,往往通过构造函数,通过研究函数的最值确定参数的范围。

练习册系列答案
相关题目
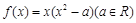 ,
,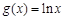 .
.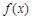 在
在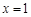 处取得极值,求
处取得极值,求 上
上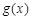 图像的上方(没有公共点),求实数
图像的上方(没有公共点),求实数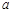 的取值范围.
的取值范围.  在
在 与
与 时都取得极值
时都取得极值 函数f(x)的极值;
函数f(x)的极值; ,方程
,方程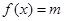 恰好有三个根,求
恰好有三个根,求 的取值范围.
的取值范围. .当
.当 时,函数
时,函数 取得极值
取得极值 .
. 有3个解,求实数
有3个解,求实数 的取值范围.
的取值范围. ,
, 为
为 的导函数.
的导函数. ,求
,求 的值;
的值; 图象与
图象与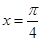 对称,△ABC的三个内角A、B、C所对的边长分别为
对称,△ABC的三个内角A、B、C所对的边长分别为 ,角A为
,角A为 ,求△ABC面积的最大值.
,求△ABC面积的最大值.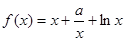 ,
, 时,求函数
时,求函数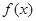 的单调增区间;
的单调增区间;
 上是减函数的充要条件;
上是减函数的充要条件;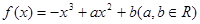
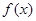 在区间(0,1)上单调递增,试求a的取值范围;
在区间(0,1)上单调递增,试求a的取值范围;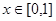 时,
时, ,试求当
,试求当 时,a的取值范围.
时,a的取值范围.