题目内容
【题目】如图,![]() ,
,![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() 的左、右焦点,直线
的左、右焦点,直线![]() ,将线段
,将线段![]() ,
,![]() 分成两段,其长度之比为
分成两段,其长度之比为![]() ,设
,设![]() 是
是![]() 上的两个动点,线段
上的两个动点,线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.

(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) ![]()
【解析】
(1)设![]() ,由线段长度之比可列出等式求出c,代入离心率公式求得a,再求出b,即可求得椭圆的标准方程;(2)当直线AB斜率不存在时,直线AB的方程为
,由线段长度之比可列出等式求出c,代入离心率公式求得a,再求出b,即可求得椭圆的标准方程;(2)当直线AB斜率不存在时,直线AB的方程为![]() ,求出P、Q坐标直接求
,求出P、Q坐标直接求![]() ;当直线AB斜率存在时,直线方程与椭圆方程联立可得关于x的一元二次方程,利用韦达定理求出
;当直线AB斜率存在时,直线方程与椭圆方程联立可得关于x的一元二次方程,利用韦达定理求出![]() 、
、![]() ,可求得
,可求得![]() 的关于m的表达式,根据题意求出m的范围即可求得
的关于m的表达式,根据题意求出m的范围即可求得![]() 的范围.
的范围.
(1)设![]() ,因为直线
,因为直线![]() ,将线段
,将线段![]() ,
,![]() 分成两段,其长度之比为
分成两段,其长度之比为![]() ,
,
所以![]() ,解得
,解得![]() ,
,
又离心率![]() ,所以
,所以![]() ,则
,则![]() ,
,
所以椭圆C的方程为:![]() ;
;
(2)①当直线AB斜率不存在时,直线AB的方程为![]() ,此时PQ与x轴重合,
,此时PQ与x轴重合,
![]() ,因为
,因为![]() ,
,![]() ,
,
所以![]() ;
;
②当直线AB斜率存在时,设直线AB的斜率为k,![]() ,
,![]() ,
,
因为M是线段AB的中点,所以![]() ,
,![]() ,
,
由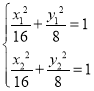 ,整理得
,整理得![]() ,
,
则![]() ,所以
,所以![]() ,此时直线PQ的斜率为
,此时直线PQ的斜率为![]() ,直线PQ的方程为:
,直线PQ的方程为:![]() 即
即![]() ,
,
设![]() ,
,
联立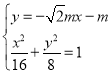 ,消去y,可得
,消去y,可得![]() ,
,
则![]() ,
,
![]() ,
,
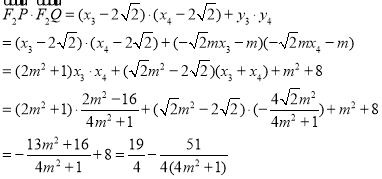
直线![]() 与椭圆
与椭圆![]() 的交点为
的交点为![]() ,
,
因为线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,则
,则![]() ,
,
![]() ,即
,即![]() .
.

【题目】某鲜花批发店每天早晨以每支2元的价格从鲜切花生产基地购入某种玫瑰,经过保鲜加工后全部装箱(每箱500支,平均每支玫瑰的保鲜加工成本为1元),然后以每箱2000元的价格整箱出售.由于鲜花的保鲜特点,制定了如下促销策略:若每天下午3点以前所购进的玫瑰没有售完,则对未售出的玫瑰以每箱1200元的价格降价处理.根据经验,降价后能够把剩余玫瑰全部处理完毕,且当天不再购进该种玫瑰.因库房限制每天最多加工6箱.
(1)若某天此鲜花批发店购入并加工了6箱该种玫瑰,在下午3点以前售出4箱,且6箱该种玫瑰被6位不同的顾客购买.现从这6位顾客中随机选取2人赠送优惠卡,求恰好一位是以2000元价格购买的顾客且另一位是以1200元价格购买的顾客的概率:
(2)此鲜花批发店统计了100天该种玫瑰在每天下午3点以前的销售量t(单位:箱),统计结果如下表所示(视频率为概率):
t/箱 | 4 | 5 | 6 |
频数 | 30 | x | s |
①估计接下来的一个月(30天)该种玫瑰每天下午3点前的销售量不少于5箱的天数并说明理由;
②记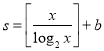 ,
,![]() ,若此批发店每天购进的该种玫瑰箱数为5箱时所获得的平均利润最大,求实数b的最小值(不考虑其他成本,
,若此批发店每天购进的该种玫瑰箱数为5箱时所获得的平均利润最大,求实数b的最小值(不考虑其他成本,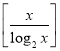 为
为![]() 的整数部分,例如:
的整数部分,例如:![]() ,
,![]() ).
).

