题目内容
【题目】若函数
， 
，则对于不同的实数
，函数
的单调区间个数不可能是（ ）
A. 1个 B. 2个 C. 3个 D. 5个
【答案】B
【解析】 由题意，(1)当
时， 
在
上为增函数，只有一个单调区间，
当
时，因为
，
所以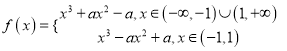
所以
（2）当
时，因为
，
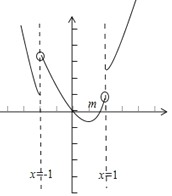
所以导数的图象如图所示，其中
为图象与
轴的交点横坐标，
所以
时， 
， 
时， 
， 
时， 
，
所以
在
时，单调递增； 
时，单调递减； 
时，单调递增，所以函数
有三个单调区间．
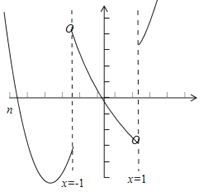
（3）当
时， 
，所以导数的图象如图所示（其中
为
时图象与
轴交点的横坐标）
所以当
时， 
，当
时， 
，
当
时， 
，当
时， 
，当
时， 
，
所以
在
时，单调递增； 
时，单调递减； 
时，单调递增， 
时，单调递减； 
时，单调递增，共有5个单调区间，
由此可得A、C、D不正确，故选B．
练习册系列答案
相关题目
【题目】某单位实行休年假制度三年以来，50名职工休年假的次数进行的调查统计结果如下表所示：
休假次数 | 0 | 1 | 2 | 3 |
人数 | 5 | 10 | 20 | 15 |
根据表中信息解答以下问题：
（1）从该单位任选两名职工，求这两人休年假次数之和为4的概率；
（2）从该单位任选两名职工，用
表示这两人休年假次数之差的绝对值，求随机变量
的分布列及数学期望
．
