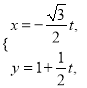题目内容
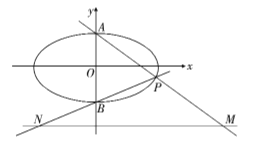
【题目】如图，已知椭圆
： 
的离心率为
，上、下顶点分别为
、
，点
在椭圆上，且异于点
、
，直线
、
与直线
： 
分别交于点
、
，且
面积的最大值为
.
（1）求椭圆
的标准方程；
（2）求线段
的长的最小值.
【答案】（1）
（2）
.
【解析】试题分析：（Ⅰ）由椭圆
： 
的离心率为
，，且
面积的最大值为
，求出a，b，由此能求出椭圆C的方程；（2）由题设可以得到直线AP的方程为y﹣1=k1（x﹣0），直线BP的方程为y﹣（﹣1）=k2（x﹣0），求出直线AP与直线l的交点M，直线BP与直线l的交点N，由此能求出线段MN长的最小值．
试题解析：
（1）当
为左右顶点时， 
最大，得
，又
， 
， 
，
（2）由题设可以得到直线
的方程为
，直线
的方程为
，
由
，由
直线
与直线
的交点
， 
直线
与直线
的交点
.
设
，则直线
的斜率
， 
的斜率
，
又点
在椭圆上，所以
，
从而有： 
.
当且仅当
即
时取等号，故线段
长的最小值是
.
练习册系列答案
相关题目
