Question

若函数f（x）在[0，1]上满足：对于任意的s，t∈[0，1]，λ＞0，都有

f(s)+λf(t)

1+λ

＜f(

s+λt

1+λ

)，则称f（x）在[0，1]上为凸函数．在三个函数f₁（x）=x+1，f₂（x）=e^x-1，f₃（x）=lg

x+1

中，在[0，1]上是凸函数的有

f₃（x）=lg

x+1

（写出您认为正确的所有函数）．

Answer 1

分析：根据凸函数的定义：对于任意的s、t∈[0，1]，λ＞0，都有

f(s)+λf(t)

1+λ

＜f(

s+λt

1+λ

)，可得它的几何意义是函数函数图象在[0，1]上的形状上凸的，如图所示．由此将三个函数图象与此定义加以对照，可得正确答案．

解答：解：根据凸函数的定义，可得
∵对于任意的s、t∈[0，1]，λ＞0，都有

f(s)+λf(t)

1+λ

＜f(

s+λt

1+λ

)，
∴对于自变量x=

s+λt

1+λ

，函数值f(

s+λt

1+λ

)要大于点A（s，f（s））与点B（t，f（t））连线段上的相应点的纵坐标

f(s)+λf(t)

1+λ

．由此可得函数在[0，1]上的函数图象是上凸的，如图所示．

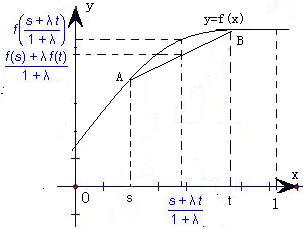
∵函数f₁（x）=x+1的图象是一条直线，函数f₂（x）=e^x-1的图象是一条下凹的曲线，
而函数f₃（x）=lg

x+1

的图象是一条上凸的曲线，
∴函数f₃（x）=lg

x+1

的在[0，1]上是凸函数．
故答案为：f₃（x）=lg

x+1

点评：本题给出凸函数的定义，要求我们从三个函数中找出符合定义的函数．着重考查了基本初等函数的图象作法及其应用等知识，属于中档题．