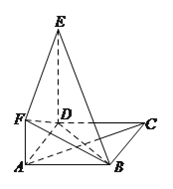
题目内容
【题目】根据下列条件求圆的方程.
(![]() )
)![]() ,
, ![]() ,
, ![]() ,三角形
,三角形![]() 的外接圆.
的外接圆.
(![]() )圆心在直线
)圆心在直线![]() 上,且与直线
上,且与直线![]() 相切于点
相切于点![]() .
.
(![]() )与
)与![]() 轴相切,圆心在直线
轴相切,圆心在直线![]() 上,且被直线
上,且被直线![]() 截得的弦长为
截得的弦长为![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】试题分析:(1)设出圆的一般式方程,将三点坐标代入得到方程组,解出方程组即可;(2)根据过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 与直线
与直线![]() 的交点即为圆心,可求出圆心坐标,进而可得半径,最后得圆的方程;(3)根据题意设圆心的坐标为
的交点即为圆心,可求出圆心坐标,进而可得半径,最后得圆的方程;(3)根据题意设圆心的坐标为![]() ,根据圆与
,根据圆与![]() 轴相切得出半径,求出弦心距
轴相切得出半径,求出弦心距![]() ,根据
,根据![]() 可解出
可解出![]() ,进而可得圆的方程.
,进而可得圆的方程.
试题解析:(![]() )设圆方程为
)设圆方程为![]() ,将
,将![]() ,
, ![]() ,
, ![]() ,
,
代入圆方程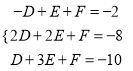 ,解得
,解得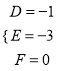 ,
,
∴圆方程为![]() .
.
(![]() )由已知:过点
)由已知:过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 与直线
与直线![]() 的交点即为圆心,∵
的交点即为圆心,∵![]() ,∴
,∴![]() 斜率为
斜率为![]() ,其方程为
,其方程为![]() ,
,
即![]() ,联立
,联立![]() 与
与![]() :
: ![]() ,解得圆心坐标为
,解得圆心坐标为![]() ,
,
∴圆半径![]() ,∴圆方程为
,∴圆方程为![]() .
.
(![]() )∵圆心在
)∵圆心在![]() 上,∴设圆心坐标为
上,∴设圆心坐标为![]() ,
,
又∵圆与![]() 轴相切,∴半径
轴相切,∴半径![]() ,弦心距
,弦心距![]() ,
,
又∵![]() 即
即![]() ,∴
,∴![]() ,
,
∴圆方程为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】某地区10名健康儿童头发和血液中的硒含量(单位:μg/ml)如下表所示:
血硒x | 74 | 66 | 88 | 69 | 91 | 73 | 66 | 96 | 58 | 73 |
发硒y | 13 | 10 | 13 | 11 | 16 | 9 | 7 | 14 | 5 | 10 |
(1)画出散点图;
(2)求回归方程;
(3)若某名健康儿童的血液中的硒含量为94 μg/ml,预测他的发硒含量.