题目内容
【题目】已知数列{an}、{bn}满足：a1= 
，an+bn=1，bn+1= 
．
（1）求a2 ， a3；
（2）证数列{ 
}为等差数列，并求数列{an}和{bn}的通项公式；
（3）设Sn=a1a2+a2a3+a3a4+…+anan+1 ， 求实数λ为何值时4λSn＜bn恒成立．
【答案】
（1）解：∵ 
，∴ 
， 
，
， 
， 
．
∴ 
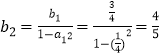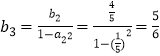（2）证明：由 
，
∴ 
= 
，
∴ 
，即an﹣an+1=anan+1，
∴ 
=1
∴数列{ 
}是以4为首项，1为公差的等差数列．
∴ 
，则 
，
∴ 
（3）解：由 ，
∴Sn=a1a2+a2a3+…+anan+1
= 
= 
= 
．
∴ 
，
要使4λSn＜bn恒成立，只需（λ﹣1）n2+（3λ﹣6）n﹣8＜0恒成立，
设f（n）=（λ﹣1）n2+3（λ﹣2）n﹣8
当λ=1时，f（n）=﹣3n﹣8＜0恒成立，
当λ＞1时，由二次函数的性质知f（n）不满足对于任意n∈N*恒成立，
当λ＜l时，对称轴n= 
f（n）在[1，+∞）为单调递减函数．
只需f（1）=（λ﹣1）n2+（3λ﹣6）n﹣8=（λ﹣1）+（3λ﹣6）﹣8=4λ﹣15＜0
∴ 
，∴λ≤1时4λSn＜bn恒成立．
综上知：λ≤1时，4λSn＜bn恒成立
【解析】（1）由给出的 ，循环代入an+bn=1和 
可求解a2 ， a3；（2）由an+bn=1得an+1+bn+1=1，结合 ，去掉bn与bn+1得到an+1与an的关系式，整理变形后可证得数列{ }是以4为首项，1为公差的等差数列，求出其通项公式后即可求得数列{an}和{ bn}的通项公式；（3）首先利用裂项求和求出Sn ， 代入4λSn＜bn ， 通过对λ分类讨论，结合二次函数的最值求使4λSn＜bn恒成立的实数λ的值．
【考点精析】根据题目的已知条件，利用等差数列的通项公式（及其变式）和等比数列的通项公式（及其变式）的相关知识可以得到问题的答案，需要掌握通项公式：
或
；通项公式：
．
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
