题目内容
13.要将甲乙两种大小不同的钢板截成A、B两种规格,每种钢板可同时截得A、B两种规格的小钢板的块数如表所示.| 规格类型 钢板类型 | A | B |
| 甲 | 2 | 1 |
| 乙 | 1 | 3 |
分析 设甲种钢板需要x张,乙种钢板需要y张;共需要z张,从而可得约束条件及目标函数,结合图象得到两种钢板的张数即可.
解答 解:设甲种钢板需要x张,乙种钢板需要y张;共需要z张;
则由题意可得,
$\left\{\begin{array}{l}{x≤5}\\{y≤10}\\{2x+y≥15}\\{x+3y≥27}\\{x,y∈N}\end{array}\right.$;
z=x+y;
作出其平面区域可得,
结合图象可得,满足条件的x,y值有:
(3,9),(3,10),(4,10),(4,8),(4,9),(5,10),(5,9),(5,8).
故z的最小值为3+9=4+8=12;
故各截两种钢板3张,9张或4张,8张时可得到所需的成品数,且使所用的两种钢板的总张数最少.
点评 本题考查了线性规划在实际问题中的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若一个圆锥的正视图(如图所示)是边长为3,3,2的三角形,则该圆锥的表面积是( )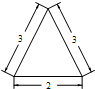

| A. | π | B. | 2π | C. | 3π | D. | 4π |
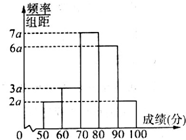 100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则测试成绩落在[60,80)中的学生人数是50.
100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则测试成绩落在[60,80)中的学生人数是50. 如图,A,B,C,D四点共圆,BC与AD的延长线交于点E,点F在BA的延长线上.
如图,A,B,C,D四点共圆,BC与AD的延长线交于点E,点F在BA的延长线上.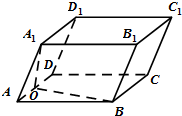 在平行六面体ABCD-A1B1C1D1中,AA1=AD=AB=2,∠A1AD=∠DAB=60°,O是AD的中点.
在平行六面体ABCD-A1B1C1D1中,AA1=AD=AB=2,∠A1AD=∠DAB=60°,O是AD的中点.