题目内容
8.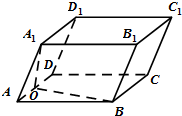 在平行六面体ABCD-A1B1C1D1中,AA1=AD=AB=2,∠A1AD=∠DAB=60°,O是AD的中点.
在平行六面体ABCD-A1B1C1D1中,AA1=AD=AB=2,∠A1AD=∠DAB=60°,O是AD的中点.(1)证明AD⊥面A1OB;
(2)当平面ABCD⊥平面AA1D1D,求VB1-CDD1.
分析 (1)证明AD⊥面A1OB,只需要证明A1O⊥AD,BO⊥AD即可;
(2)利用A1B1∥平面CDD1C1,可得${V_{{B_1}-CD{D_1}}}={V_{{A_1}-CD{D_1}}}={V_{C-{A_1}{D_1}D}}=\frac{1}{6}{V_{ABCD-{A_1}{B_1}{C_1}{D_1}}}$,即可求VB1-CDD1.
解答 (1)证明:∵AA1=AD,∠A1AD=60°,
∴A1O⊥AD
同理BO⊥AD
∵A1O∩BO=O
∴AO⊥平面A1BO,即AD⊥面A1OB;
(2)解:∵A1B1∥平面CDD1C1
∴${V_{{B_1}-CD{D_1}}}={V_{{A_1}-CD{D_1}}}={V_{C-{A_1}{D_1}D}}=\frac{1}{6}{V_{ABCD-{A_1}{B_1}{C_1}{D_1}}}$
由(1)A1O⊥AD,
又平面ABCD⊥平面AA1D1D
∴A1O⊥平面ABCD
∵${A_1}O=\sqrt{3}$,${S_{ABCD}}=AB•ADsin60°=2\sqrt{3}$
∴${V_{ABCD-{A_1}{B_1}{C_1}{D_1}}}={A_1}O•{S_{ABCD}}=6$
∴${V_{{B_1}-CD{D_1}}}=\frac{1}{6}×6=1$
点评 本题考查线面垂直、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.要将甲乙两种大小不同的钢板截成A、B两种规格,每种钢板可同时截得A、B两种规格的小钢板的块数如表所示.
已知库房中现有甲乙两种钢板的数量分别为5张和10张,市场急需AB两种规格的成品数分别为15块和27块,问各截两种钢板多少张可得到所需的成品数,且使所用的两种钢板的总张数最少?
| 规格类型 钢板类型 | A | B |
| 甲 | 2 | 1 |
| 乙 | 1 | 3 |
