题目内容
(本小题满分12分)已知数列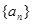 的前n项和
的前n项和 满足
满足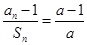 (
( >0,且
>0,且 )。数列
)。数列 满足
满足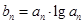
(I)求数列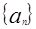 的通项。
的通项。
(II)若对一切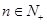 都有
都有 ,求
,求 的取值范围。
的取值范围。
(1)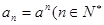 (2)
(2)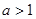 或
或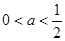
解析试题分析:解:(1)由题意可知当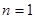 时,
时, ………………………………2分
………………………………2分
当 时,
时, (1)
(1)
 (2)
(2)
用(1)式减去(2)式得: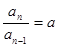
所以数列 是等比数列 所以
是等比数列 所以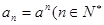 )…………………………6分
)…………………………6分
(2)因为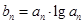 所以
所以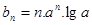
当对一切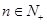 都有
都有 即有
即有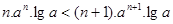
(1)当 有
有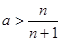 当对一切
当对一切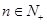 都成立所以
都成立所以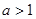 ……9分
……9分
(2)当 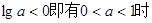 有
有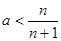 当对一切
当对一切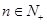 都成立所以有
都成立所以有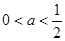
 ………………………………………………11分
………………………………………………11分
综合以上可知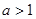 或
或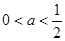 ………………………………12分
………………………………12分
考点:本试题考查的数列的通项公式,以及单调性性质。
点评:对于数列的通项公式的求解,一般可以通过前n项和与通项公式的关系来解得,也可以利用递推关系来构造特殊的等差或者等比数列来求解。而对于数列的单调性的证明,一般只能用定义法来说明,进而得到参数的范围,属于中档题。

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
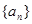 的前
的前 项和为
项和为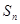 ,且满足
,且满足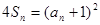 (
(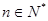 ).
).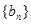 的通项公式为
的通项公式为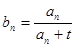 (
(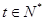 ),若
),若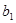 ,
,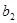 ,
,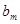 (
(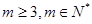 )成等差数列,求
)成等差数列,求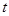 和
和 的值;
的值;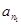 ,
,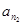 ,
,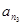 .
.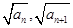 )在双曲线y2-x2=1上,点(
)在双曲线y2-x2=1上,点(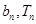 )在直线y=-
)在直线y=-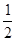 x+1上,其中Tn是数列{bn}的前n项和。
x+1上,其中Tn是数列{bn}的前n项和。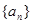 的首项为
的首项为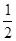 ,
,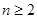 时,
时,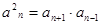 ,数列
,数列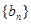 对任意
对任意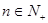 均有
均有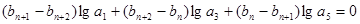
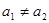 ,求证:数列
,求证:数列 ,数列
,数列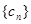 满足
满足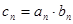 ,记数列
,记数列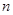 项和为
项和为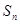 ,求证
,求证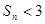 .
.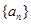 前
前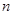 项和
项和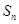 满足
满足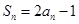 ,等差数列
,等差数列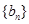 满足
满足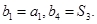
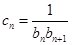 ,数列
,数列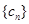 的前
的前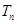 ,问
,问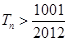 的最小正整数n是多少?
的最小正整数n是多少?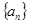 是递增数列,且满足
是递增数列,且满足 。
。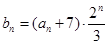 ,求数列
,求数列 的前
的前 项和
项和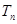 。
。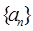 中,
中,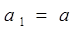 ,
, 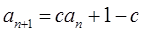
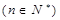
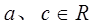
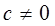
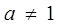 时,
时, 是等比数列,并求
是等比数列,并求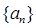 通项公式。
通项公式。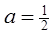 ,
,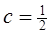 ,
,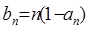
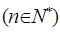 求:数列
求:数列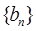 的前n项的和
的前n项的和 。
。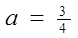 、
、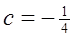 、
、 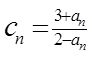 。记
。记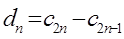 ,数列
,数列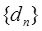 的前n项和
的前n项和 。证明:
。证明: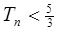
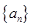 是等差数列,其中
是等差数列,其中 .
.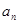 ;
;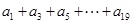 值.
值.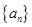 的前
的前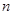 项和是
项和是 ,且
,且 .
.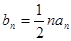 ,求数列
,求数列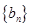 的前
的前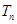 .
.