题目内容
(本小题满分13分)已知数列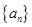 的前
的前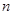 项和是
项和是 ,且
,且 .
.
(Ⅰ)求数列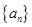 的通项公式;
的通项公式;
(Ⅱ)记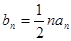 ,求数列
,求数列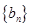 的前
的前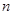 项和
项和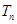 .
.
(Ⅰ) ; (Ⅱ)
; (Ⅱ) 。
。
解析试题分析:(I)先令n=1,得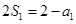 ,从而得到
,从而得到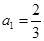 .
.
然后再令 时,由
时,由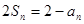 得:
得: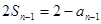 ,两式相减得:
,两式相减得:
即 ,从而确定
,从而确定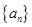 为等比数列,问题得解.
为等比数列,问题得解.
(II)在(I)的基础上,可求出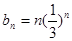 ,显然应采用错位相减的方法求和即可.
,显然应采用错位相减的方法求和即可.
(Ⅰ)当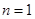 时,
时, 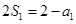 ,
,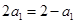 ,∴
,∴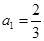 ; ………… 2分
; ………… 2分
当 时,由
时,由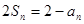 得:
得: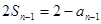
两式相减得:
即 ,又
,又
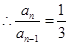
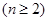 , ……………… 5分
, ……………… 5分
∴数列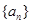 是以
是以 为首项,
为首项,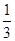 为公比的等比数列. ………………… 6分
为公比的等比数列. ………………… 6分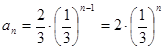 ………………… 7分
………………… 7分
(Ⅱ)由(Ⅰ)知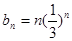 , ………………… 8分
, ………………… 8分
∴ …………………①
…………………①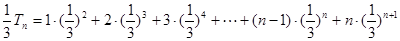 …………②
…………②
由①-②得: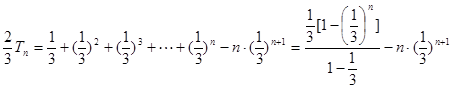
…………………9分 ………………… 12分
………………… 12分 ………………… 13分
………………… 13分
考点: 由an与Sn的关系求出an,等比数列的定义,通项公式,错位相减法求和.
点评:(I)再由Sn求an时,应先确定a1,然后再根据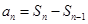 ,求
,求 时,an.
时,an.
(II)当一个数列的通项是一个等差数列与一个等比数列积时,可以采用错位相减法求和.

练习册系列答案
相关题目
设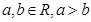 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A.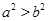 | B.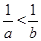 | C.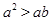 | D. |
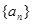 的前n项和
的前n项和 满足
满足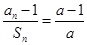 (
( >0,且
>0,且 )。数列
)。数列 满足
满足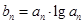
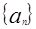 的通项。
的通项。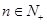 都有
都有 ,求
,求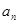 }满足
}满足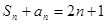 ,
, 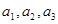 ,并推测
,并推测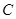 :
: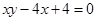 ,数列
,数列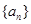 的首项
的首项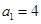 ,且当
,且当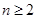 时,点
时,点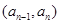 恒在曲线
恒在曲线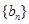 满足
满足 。
。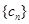 满足
满足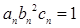 ,试比较数列
,试比较数列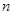 项和
项和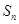 与2的大小。
与2的大小。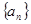 的前
的前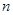 项和为
项和为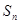 ,满足
,满足 .
. ;
;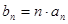 ,求数列
,求数列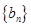 的前
的前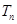 .
.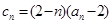 ,若对任意的正整数
,若对任意的正整数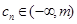 ,求实数
,求实数 的取值范围.
的取值范围.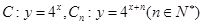 ,从
,从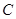 上的点
上的点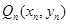 作
作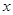 轴的垂线,交
轴的垂线,交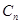 于点
于点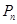 ,再从点
,再从点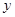 轴的垂线,交
轴的垂线,交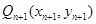 ,设
,设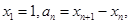
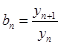
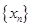 的通项公式;
的通项公式; 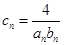 ,数列
,数列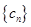 的前
的前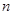 项和为
项和为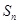 ,试比较
,试比较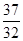 的大小
的大小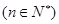 ;
;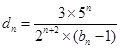 ,数列
,数列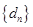 的前
的前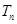 ,试证明:
,试证明: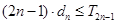
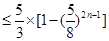
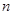 个图形包含
个图形包含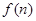 个小正方形.
个小正方形.
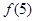 的值;
的值; 与
与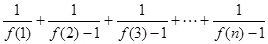 的值.
的值.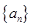 是公差为2的等差数列,
是公差为2的等差数列,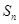 是
是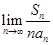 = .
= .