题目内容
已知函数 若存在函数
若存在函数 使得
使得 恒成立,则称
恒成立,则称 是
是 的一个“下界函数”.
的一个“下界函数”.
(I) 如果函数 为实数
为实数 为
为 的一个“下界函数”,求
的一个“下界函数”,求 的取值范围;
的取值范围;
(Ⅱ)设函数 试问函数
试问函数 是否存在零点,若存在,求出零点个数;若不存在,请说明理由.
是否存在零点,若存在,求出零点个数;若不存在,请说明理由.
(I)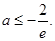 (Ⅱ)函数
(Ⅱ)函数 不存在零点.
不存在零点.
解析试题分析:(I)解法一:由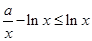 得
得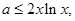 1分
1分
记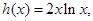 则
则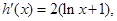 2分
2分
当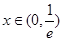 时,
时,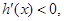 所以
所以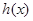 在
在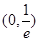 上是减函数,
上是减函数,
当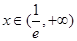 时,
时,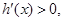 所以
所以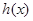 在
在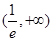 上是增函数, 3分
上是增函数, 3分
因此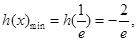 即
即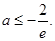 5分
5分
解法二:由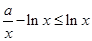 得
得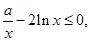
设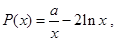 则
则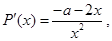 1分
1分
(1)若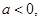 由
由 知
知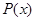 在
在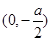 上是增函数,在
上是增函数,在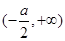 上是减函数, 2分
上是减函数, 2分
因为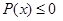 恒成立,所以
恒成立,所以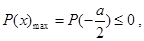 解得
解得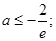 3分
3分
(2)若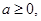 当
当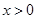 且
且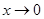 时,
时,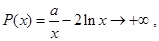
此与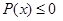 恒成立矛盾,故舍去
恒成立矛盾,故舍去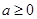 ; 4分
; 4分
综上得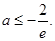 5分
5分
(Ⅱ)解法一:函数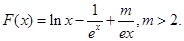
由(I)知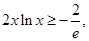 即
即 6分
6分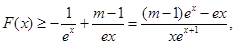 7分
7分
设函数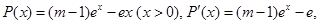
(1)当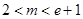 时,
时,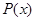 在
在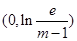 上是减函数,在
上是减函数,在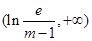 上是增函数,
上是增函数,
故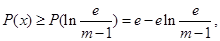
因为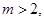 所以
所以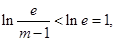 即
即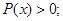 8分
8分
(2)当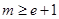 时,
时,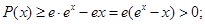 9分
9分
综上知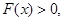 所以函数
所以函数 不存在零点. 10分
不存在零点. 10分
解法二:前同解法一,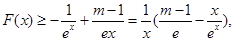 7分
7分
记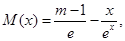 则
则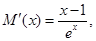
所以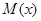 在
在 上是减函数,在
上是减函数,在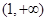 上是增函数,
上是增函数,
因此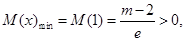 &nbs
&nbs

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
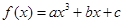
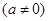 为奇函数,其图象在点
为奇函数,其图象在点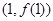 处的切线与直线
处的切线与直线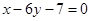 垂直,导函数
垂直,导函数 的最小值为
的最小值为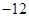 .
.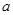 ,
,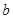 ,
,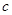 的值;
的值;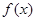 的单调递增区间,并求函数
的单调递增区间,并求函数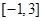 上的最大值和最小值.
上的最大值和最小值.
 在
在 和
和 处的切线互相平行,求
处的切线互相平行,求 的值及函数
的值及函数 的单调区间;
的单调区间; ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求实数
,求实数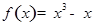 .
. 在点
在点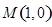 处的切线方程;
处的切线方程;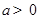 ,如果过点
,如果过点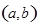 可作曲线
可作曲线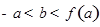
 ,试比较
,试比较 与
与 的大小;
的大小; ,使得
,使得 对任意大于
对任意大于 的自然数
的自然数 都成立?若存在,试求出
都成立?若存在,试求出 的值并证明你的结论;若不存在,请说明理由。
的值并证明你的结论;若不存在,请说明理由。 ,
, .(其中
.(其中 为自然对数的底数).
为自然对数的底数).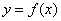 在
在 处的切线与直线
处的切线与直线 垂直,求
垂直,求 的值;
的值; ≥0,
≥0, 恒成立,试确定实数
恒成立,试确定实数 时,是否存在实数
时,是否存在实数 ,使曲线C:
,使曲线C: 在点
在点 处的切线与
处的切线与 轴垂直?若存在,求出
轴垂直?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 
 。
。 的最小值;
的最小值; 
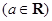 ,讨论函数
,讨论函数 的单调性;
的单调性; 的直线与曲线
的直线与曲线 交于
交于 ,
,
 两点,求证:
两点,求证: 。
。
 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围; 时,求
时,求 上的最大值和最小值.
上的最大值和最小值.