题目内容
7.有一直三棱柱的三视图如图所示: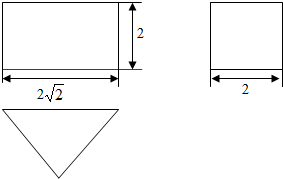
则该三棱柱的侧面积为4$\sqrt{2}$+4$\sqrt{6}$.
分析 根据几何体的三视图,得出该几何体是底面为等腰三角形的直三棱柱,结合图中数据求出它的侧面积.
解答 解:根据几何体的三视图,得;
该几何体是底面为等腰三角形的直三棱柱,
且三角形的底边为2$\sqrt{2}$,对应边上的高为2,
三棱柱的高为2;
所以该四棱柱的侧面积为
2$\sqrt{2}$×2+2×2×$\sqrt{{(\sqrt{2})}^{2}{+2}^{2}}$=4$\sqrt{2}$+4$\sqrt{6}$.
故答案为:4$\sqrt{2}$+4$\sqrt{6}$.
点评 本题考查了利用空间几何体的三视图求面积的应用问题,是基础题目.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
16.n为整数,化简$\frac{sin(nπ-α)}{cos(nπ-α)}$所得结果是( )
| A. | tannα | B. | -tannα | C. | tanα | D. | -tanα |
17.已知定义在R上的奇函数f(x)满足f(x-1)=f(x+1),当x∈(0,1]时,f(x)=x+3,则f(-$\frac{5}{2}$)=( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{7}{2}$ | C. | -2 | D. | $\frac{7}{2}$ |