题目内容
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M是A1B的中点.
(Ⅰ)在线段B1C1上是否存在一点N,使得MN⊥平面A1BC?若存在,找出点N的位置幷证明;若不存在,请说明理由;
(Ⅱ)求平面A1AB和平面A1BC所成角的大小.
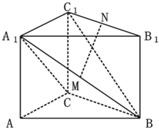
(Ⅰ)在线段B1C1上是否存在一点N,使得MN⊥平面A1BC?若存在,找出点N的位置幷证明;若不存在,请说明理由;
(Ⅱ)求平面A1AB和平面A1BC所成角的大小.

(Ⅰ)根据题意CA、CB、CC1两两互相垂直
如图:以C为原点,CA、CB、CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系
设AC=BC=CC1=a,则A1(a,0,a),M(
,
,
),B(0,a,0),B1(0,a,a),A(a,0,0),C1(0,0,a),
假设在B1C1上存在一点N,使MN⊥平面A1BC,设N(0,y,a)
所以
=(a,-a,a),
=(a,0,a),
=(-
,y-
,
)
由
•
=0,
•
=0,得:y=
∴N在线段B1C1的中点处(6分)
(Ⅱ)由(Ⅰ)知MN⊥平面A1BC,则平面A1BC的一个法向量为
=(1,0,-1)分
取AB中点D,连接CD,易证CD⊥平面A1AB
∴可得面A1AB的一个法向量
=(
,
,0)(8分)
cos?
,
>=
=
=
所以面A1AB和面A1BC所成的角为
.(12分)
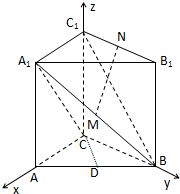
如图:以C为原点,CA、CB、CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系
设AC=BC=CC1=a,则A1(a,0,a),M(
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
假设在B1C1上存在一点N,使MN⊥平面A1BC,设N(0,y,a)
所以
| BA1 |
| CA1 |
| MN |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
由
| MN |
| BA1 |
| MN |
| CA1 |
| a |
| 2 |
∴N在线段B1C1的中点处(6分)
(Ⅱ)由(Ⅰ)知MN⊥平面A1BC,则平面A1BC的一个法向量为
| n |
取AB中点D,连接CD,易证CD⊥平面A1AB
∴可得面A1AB的一个法向量
| n1 |
| 1 |
| 2 |
| 1 |
| 2 |
cos?
| n |
| n1 |
| ||||
|
|
| ||||||
|
| 1 |
| 2 |
所以面A1AB和面A1BC所成的角为
| π |
| 3 |


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的底面是直角三角形,
的底面是直角三角形, ,点
,点 在底面内的射影恰好是
在底面内的射影恰好是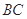 的中点,且
的中点,且


 平面
平面 ;
; ,求点
,求点 到平面
到平面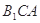 的距离.
的距离.


