Question

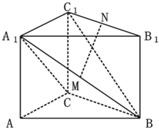
如图，在长方体ABCD-A₁B₁C₁D₁中，AD=AA₁=1，AB=2．E是CC₁的中点，
（1）求锐二面角D-B₁E-B的余弦值．
（2）试判断AC与面DB₁E的位置关系，并说明理由．
（3）设M是棱AB上一点，若M到面DB₁E的距离为

21

7

，试确定点M的位置．

Answer 1

建如图的立空间坐标系可得：D（0，0，0），A（1，0，0），C（0，2，0），B（1，2，0），A₁（1，0，1），D₁（0，0，1），C₁（0，2，1），B₁（1，2，1），由中点坐标公式可得E（0，2，

1

2

），
（1）设面DB₁E的法向量是

n1

=(x，y，z)，又

DE

=（0，2，

1

2

），

DB1

=（1，2，1），由

n1 • DE =0 n1 • DB1 =0

得

2y+ 1 2 z=0 x+2y+z=0

，令y=1，得x=2，z=-4
故有

n1

=(2，1，-4)，同理可求得面BB₁E的法向量为

n2

=(0，1，0)，故两平面所成的税二面角的余弦cosθ=|

n1 • n2

| n1 || n2 |

|=

1

21

（2）由题意，AC的方向向量的坐标是

AC

=（-1，2，0），又面DB₁E的法向量

n1

=(2，1，-4)，由于

AC

•

n1

=-2+2=0，故

AC

⊥

n1

，又AC不在面DB₁E内，故AC与面DB₁E的位置关系是平行．
（3）M是棱AB上一点，
设M（1，x，0），则

MD

=（-1，-X，0），
由（1）面DB₁E的法向量

n1

=(2，1，-4)，M到面DB₁E的距离即向量

MD

在DB₁E的法向量

n1

上的投影长度，
故有d=|

n1 • MD

| n1 |

|=|

-2-X

21

=|

21

7

|即得|2+x|=3解得x=1，或x=-1（由图知，此结论舍），
故M是AB的中点时，符合题意．