题目内容
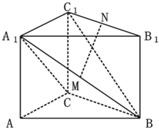
已知平面四边形ABCD的对角线AC,BD交于点O,AC⊥BD,且BA=BC=4,DA=DC=2
,∠ABC=60°.现沿对角线AC将三角形DAC翻折,使得平面DAC⊥平面BAC.翻折后:
(Ⅰ)证明:AC⊥BD;
(Ⅱ)记M,N分别为AB,DB的中点.①求二面角N-CM-B大小的余弦值;②求点B到平面CMN的距离.

| 3 |
(Ⅰ)证明:AC⊥BD;
(Ⅱ)记M,N分别为AB,DB的中点.①求二面角N-CM-B大小的余弦值;②求点B到平面CMN的距离.

(Ⅰ)证明:因为AC⊥BD,且BA=BC=4,DA=DC=2
,
所以0为AC的中点,
所以AC⊥DO,AC⊥OB,所以AC⊥面BOD,所以AC⊥BD.
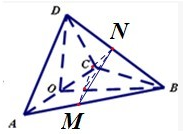
(II)①因为平面DAC⊥平面BAC.所以D0⊥面ABC.
以O为坐标原点,以OA,OB,OD分别为x,y,z轴建立空间坐标系,
则A(2,0,0),C(-2,0,0),B(0,2
,0),D(0,0,2
),
则M(1,
,0),N(0,
,
).则
=(3,
,0),
=(-1,0,
).
则平面BCM的法向量为
=(0,0,1),
设平面NCM的法向量为
=(x,y,z),则
,
即
,令z=
,则x=2,y=-2
.即
=(2,-2
,
).
所以cosθ=cos<
,
>=
=
=
=
,
所以二面角N-CM-B大小的余弦值为
.
②
=(-1,
,0),平面NCM的法向量为
=(2,-2
,
).
点B到平面CMN的距离d=
=
=
=
,
故点B到平面CMN的距离为
.
| 3 |
所以0为AC的中点,
所以AC⊥DO,AC⊥OB,所以AC⊥面BOD,所以AC⊥BD.
(II)①因为平面DAC⊥平面BAC.所以D0⊥面ABC.
以O为坐标原点,以OA,OB,OD分别为x,y,z轴建立空间坐标系,
则A(2,0,0),C(-2,0,0),B(0,2
| 3 |
| 2 |
则M(1,
| 3 |
| 3 |
| 2 |
| CM |
| 3 |
| MN |
| 2 |
则平面BCM的法向量为
| n |
设平面NCM的法向量为
| m |
|
即
|
| 2 |
| 3 |
| m |
| 3 |
| 2 |
所以cosθ=cos<
| m |
| n |
| ||||
|
|
| ||||||
|
| ||
|
| 1 |
| 3 |
所以二面角N-CM-B大小的余弦值为
| 1 |
| 3 |
②
| MB |
| 3 |
| m |
| 3 |
| 2 |
点B到平面CMN的距离d=
|
| ||||
|
|
|-2-2
| ||||||
|
| 8 | ||
|
4
| ||
| 3 |
故点B到平面CMN的距离为
4
| ||
| 3 |


练习册系列答案
相关题目