Question

【题目】在平面直角坐标系xOy中，已知椭圆离心率是，焦点到相应准线的距离是3．

（1）求椭圆的方程；

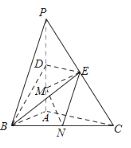
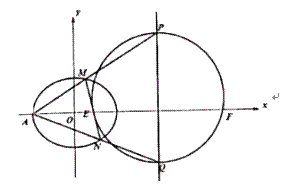
（2）如图，设A是椭圆的左顶点，动圆过定点E（1，0）和F（7，0），且与直线x＝4交于点P，Q．

①求证：AP，AQ斜率的积是定值；

②设AP，AQ分别与椭圆交于点M，N，求证：直线MN过定点．

Answer 1

【答案】（1）；（2）①见解析；②见解析.

【解析】

(1)由椭圆的离心率得到，结合焦点到相应准线的距离可求出的值，进而求出的值，即可得出椭圆的方程；(2) ①设动圆圆心坐标为 ,进而写出动圆的方程，将直线的方程代入圆的方程，得出点两点的纵坐标之积，再利用斜率公式可得出的斜率之积为定值；②设直线的方程为，将直线的方程与椭圆的方程联立，可得，由两点的纵坐标之积为 ,结合韦达定理计算出，从而得出直线过定点.

（1）设椭圆的焦距为，由题意可得，所以，，

因为椭圆的焦点到相应准线的距离为，得c=1，所以，，

因此，椭圆的方程为；

（2）①设动圆的圆心坐标为，则圆的方程为，

设点，令，可得，

则AP、AQ的斜率之积为（定值）；

②设直线MN的方程为，设点

将直线MN的方程代入椭圆方程并化简得，

由韦达定理可得

因为A、M、P三点共线，则，

由于，，

所以，则，同理可得

由

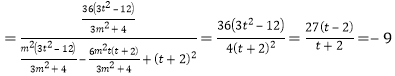，解得t=1，

因此，直线MN过定点（1，0）.