题目内容
先后2次抛掷一枚骰子,将得到的点数分别记为 .
.
(1)求直线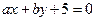 与圆
与圆 相切的概率;
相切的概率;
(2)将 的值分别作为三条线段的长,试列举出这三条线段能围成等腰三角形的所有情形并求其概率.
的值分别作为三条线段的长,试列举出这三条线段能围成等腰三角形的所有情形并求其概率.
 .
.(1)求直线
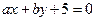 与圆
与圆 相切的概率;
相切的概率;(2)将
 的值分别作为三条线段的长,试列举出这三条线段能围成等腰三角形的所有情形并求其概率.
的值分别作为三条线段的长,试列举出这三条线段能围成等腰三角形的所有情形并求其概率. ,
,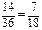
解:(1)先后2次抛掷一枚骰子,将得到的点数分别记为 事件总数为
事件总数为
 --------------------2分
--------------------2分
∵直线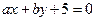 与圆
与圆 相切的充要条件是
相切的充要条件是
 即:
即: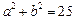 ,由于
,由于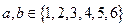
∴满足条件的情况只有a=3,b=4,;
或a=4,b=3,两种情况. ---------------------------4分
∴直线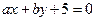 与圆x2+y2=1相切的概率是
与圆x2+y2=1相切的概率是 ---------------5分
---------------5分
(2)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,事件总数为 .
.
∵三角形的一边长为5
∴当a=1时,b=5,(1,5,5) 1种 ------------6分
当a=2时,b=5,(2,5,5) 1种 ------------7分
当a=3时,b=3,5,(3,3,5),(3,5,5) 2种 ----------8分
当a=4时,b=4,5,(4,4,5),(4,5,5) 2种 -------------9分
当a=5时,b=1,2,3,4,5,6,(5,1,5),(5,2,5),(5,3,5),
(5,4,5),(5,5,5),(5,6,5) 6种 ------------------10分
当a=6时,b=5,6,(6,5,5),(6,6,5) 2种 ---------------------11分
故满足条件的不同情况共有14种
答:三条线段能围成不同的等腰三角形的概率为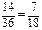 . -----12分
. -----12分
 事件总数为
事件总数为 --------------------2分
--------------------2分∵直线
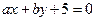 与圆
与圆 相切的充要条件是
相切的充要条件是 即:
即: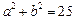 ,由于
,由于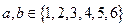
∴满足条件的情况只有a=3,b=4,;
或a=4,b=3,两种情况. ---------------------------4分
∴直线
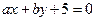 与圆x2+y2=1相切的概率是
与圆x2+y2=1相切的概率是 ---------------5分
---------------5分(2)先后2次抛掷一枚骰子,将得到的点数分别记为a,b,事件总数为
 .
.∵三角形的一边长为5
∴当a=1时,b=5,(1,5,5) 1种 ------------6分
当a=2时,b=5,(2,5,5) 1种 ------------7分
当a=3时,b=3,5,(3,3,5),(3,5,5) 2种 ----------8分
当a=4时,b=4,5,(4,4,5),(4,5,5) 2种 -------------9分
当a=5时,b=1,2,3,4,5,6,(5,1,5),(5,2,5),(5,3,5),
(5,4,5),(5,5,5),(5,6,5) 6种 ------------------10分
当a=6时,b=5,6,(6,5,5),(6,6,5) 2种 ---------------------11分
故满足条件的不同情况共有14种
答:三条线段能围成不同的等腰三角形的概率为
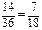 . -----12分
. -----12分
练习册系列答案
相关题目
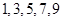 ,从这5条线段中任取3条,则所取3条线段能构成一三角形的概率
,从这5条线段中任取3条,则所取3条线段能构成一三角形的概率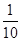
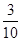
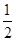
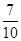
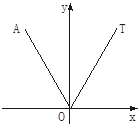
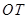 落在
落在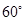 的终边上,任作一条射线
的终边上,任作一条射线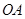 ,则射线落在∠
,则射线落在∠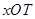 内的概率是( ).
内的概率是( ).



 (1)若
(1)若 ,求
,求 的概率;
的概率; ,求
,求 之间的概率。
之间的概率。 内的所有实数中,随机地取一个实数
内的所有实数中,随机地取一个实数 ,求实数
,求实数 的概率
的概率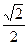 B.
B. 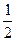
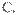
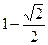 D.
D. 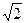
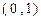 的随机数,则其体对角线的长小于
的随机数,则其体对角线的长小于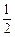 的概率为: 。
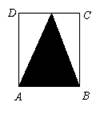
的概率为: 。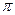 ,宽为2的矩形
,宽为2的矩形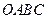 内,曲线
内,曲线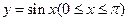 与
与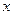 轴围成如图所示的阴影部分,向矩形
轴围成如图所示的阴影部分,向矩形