题目内容
3.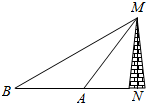 如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )
如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )| A. | 100$\sqrt{2}$m | B. | 100$\sqrt{3}$m | C. | 100m | D. | 200m |
分析 判断三角形ABM是等腰三角形,推出AM=AB=200,在三角形AMN中求解即可.
解答 解:如图,在三角形ABM中,∵∠B=30°,∠BAM=120°,∴∠AMB=30°,
∴三角形ABM是等腰三角形,∴AM=AB=200(米),
电视塔的高度MN=AMsin∠MAN=200sin60°=100$\sqrt{3}$(米).
故选B.
点评 本题考查三角形的解法以及实际应用,考查计算能力.

练习册系列答案
相关题目
13.从0,8中任取一数,从3,5,7中任取两个数字组成无重复数字的三位数,其中奇数的个数为( )
| A. | 24 | B. | 18 | C. | 12 | D. | 6 |
18.如图,将圆沿AB折叠后,圆弧恰好经过圆心,则∠AOB的度数等于( )
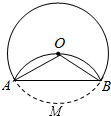

| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
13.直线xcos140°+ysin140°-2=0的倾斜角是( )
| A. | 40° | B. | 50° | C. | 130° | D. | 140° |
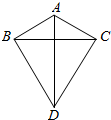 如图,在△ABC中,AB=AC=a,以BC为边向外作正三角形BCD,则AD的最大值为2a.
如图,在△ABC中,AB=AC=a,以BC为边向外作正三角形BCD,则AD的最大值为2a.