题目内容
14.已知函数f(x)=ax-$\frac{a}{x}$-lnx,a∈R(1)若a=1,求f(x)的单调增区间;
(2)若函数f(x)为单调递增函数,求a的取值范围;
(3)若m≥n>0,求证:2(m-n)≥$\sqrt{mn}$(lnm-lnn)
分析 (1)若a=1,求出函数的导数,即可f(x)的单调增区间;
(2)若函数f(x)为单调递增函数,转化为f′(x)≥0成立,解不等式即可求a的取值范围;
(3)利用分析法进行证明即可.
解答 解:(1)若a=1,f(x)=x-$\frac{1}{x}$-lnx,
函数的定义域为(0,+∞),
则f′(x)=1+$\frac{1}{{x}^{2}}$-$\frac{1}{x}$=$\frac{{x}^{2}-x+1}{{x}^{2}}$=$\frac{(x-\frac{1}{2})^{2}+\frac{3}{4}}{{x}^{2}}$>0,
∴函数f(x)在(0,+∞)上为增函数,
即f(x)的单调增区间为(0,+∞);
(2)若函数f(x)为单调递增函数,
则f′(x)≥0成立,
f′(x)=a+$\frac{a}{{x}^{2}}$-$\frac{1}{x}$=$\frac{a{x}^{2}-x+a}{{x}^{2}}$≥0,
即ax2-x+a≥0在(0,+∞)上恒成立,
即a(x2+1)≥x,a≥$\frac{x}{{x}^{2}+1}$在(0,+∞)上恒成立,
∵$\frac{x}{{x}^{2}+1}$=$\frac{1}{x+\frac{1}{x}}≤\frac{1}{2\sqrt{x•\frac{1}{x}}}=\frac{1}{2}$,当且仅当x=$\frac{1}{x}$,即x=1时取等号,
∴a≥$\frac{1}{2}$,即a的取值范围是[$\frac{1}{2}$,+∞);
(3)∵m≥n>0,
∴$\sqrt{\frac{m}{n}}≥1,\sqrt{mn}>0$,
∴要证2(m-n)≥$\sqrt{mn}$(lnm-lnn)
只需要证明$\frac{m-n}{\sqrt{mn}}$≥$\frac{lnm-lnn}{2}$,
只需要证$\sqrt{\frac{m}{n}}$$-\sqrt{\frac{n}{m}}$$≥\frac{1}{2}ln\frac{m}{n}$=ln$\sqrt{\frac{m}{n}}$,
只需要证$\sqrt{\frac{m}{n}}$$-\sqrt{\frac{n}{m}}$-ln$\sqrt{\frac{m}{n}}$≥0,
由(1)可知当x>0时,f(x)=x-$\frac{1}{x}$-lnx为增函数,
∴f($\sqrt{\frac{m}{n}}$)≥f(1),
∴$\sqrt{\frac{m}{n}}$$-\sqrt{\frac{n}{m}}$-ln$\sqrt{\frac{m}{n}}$=$\sqrt{\frac{m}{n}}$-$\frac{1}{\sqrt{\frac{m}{n}}}$-ln$\sqrt{\frac{m}{n}}$≥1-1-ln1=0,
∴$\sqrt{\frac{m}{n}}$$-\sqrt{\frac{n}{m}}$-ln$\sqrt{\frac{m}{n}}$≥0,
故原不等式成立.
点评 本题主要考查函数单调性的判断和应用以及不等式的证明,考查学生的推理和运算能力,综合性较强,有一定的难度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 命题“?x∈R,ex>0”的否定是“?x∈R,ex>0” | |
| B. | 命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题 | |
| C. | “x2+2x≥ax在x∈[1,2]上恒成立”?“对于x∈[1,2],有(x2+2x)min≥(ax)max” | |
| D. | 命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题 |
| A. | 3 | B. | 6 | C. | 13 | D. | 26 |
| A. | -$\frac{1}{2}\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}$ | B. | $\frac{1}{2}\overrightarrow{a}-\frac{1}{4}\overrightarrow{b}$ | C. | $\frac{1}{2}\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}$ | D. | -$\frac{1}{2}\overrightarrow{a}-\frac{1}{4}\overrightarrow{b}$ |
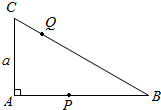 如图,在Rt△ABC中,∠B=30°,∠C=60°,AC=a,动点P,Q自A出发分别沿边界按ABCA的方向及ACBA的方向运动,它们的速度之比是1:3,当P,Q相遇时,停止运动,点P所走过的路程为x,△APQ的面积为y,写出y关于x的函数关系式,并求出定义域.
如图,在Rt△ABC中,∠B=30°,∠C=60°,AC=a,动点P,Q自A出发分别沿边界按ABCA的方向及ACBA的方向运动,它们的速度之比是1:3,当P,Q相遇时,停止运动,点P所走过的路程为x,△APQ的面积为y,写出y关于x的函数关系式,并求出定义域.