题目内容
13.已知4|x+2|-|x-1|≥3,则求得x的取值范围是{x|x≤-4,或x≥-$\frac{4}{5}$}.分析 把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
解答 解:4|x+2|-|x-1|≥3,等价于$\left\{\begin{array}{l}{x<-2}\\{-4(x+2)-(1-x)≥3}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{-2≤x<1}\\{4(x+2)-(1-x)≥3}\end{array}\right.$②,或 $\left\{\begin{array}{l}{x≥1}\\{4(x+2)-(x-1)≥3}\end{array}\right.$③.
解①求得x≤-4,解②求得-$\frac{4}{5}$≤x<1,解③求得 x≥1.
综上可得,原不等式的解集为{x|x≤-4,或x≥-$\frac{4}{5}$},
故答案为:{x|x≤-4,或x≥-$\frac{4}{5}$}.
点评 本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列说法中正确的是( )
| A. | 命题“?x∈R,ex>0”的否定是“?x∈R,ex>0” | |
| B. | 命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题 | |
| C. | “x2+2x≥ax在x∈[1,2]上恒成立”?“对于x∈[1,2],有(x2+2x)min≥(ax)max” | |
| D. | 命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题 |
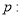 实数
实数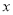 满足
满足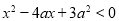 ,其中
,其中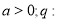 实数
实数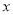 满足
满足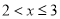 .
. ,且
,且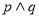 为真,求实数
为真,求实数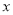 的取值范围;
的取值范围;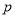 是
是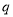 的必要不充分条件,求实数
的必要不充分条件,求实数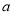 的取值范围.
的取值范围.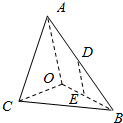 如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.
如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.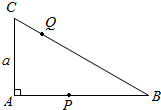 如图,在Rt△ABC中,∠B=30°,∠C=60°,AC=a,动点P,Q自A出发分别沿边界按ABCA的方向及ACBA的方向运动,它们的速度之比是1:3,当P,Q相遇时,停止运动,点P所走过的路程为x,△APQ的面积为y,写出y关于x的函数关系式,并求出定义域.
如图,在Rt△ABC中,∠B=30°,∠C=60°,AC=a,动点P,Q自A出发分别沿边界按ABCA的方向及ACBA的方向运动,它们的速度之比是1:3,当P,Q相遇时,停止运动,点P所走过的路程为x,△APQ的面积为y,写出y关于x的函数关系式,并求出定义域.