Question

【题目】（本小题满分12分）如图,在平面直角坐标系中, 已知分别是椭圆的左、右焦点分别是椭圆的左、右顶点,为线段的中点, 且.

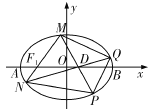
（1）求椭圆的方程；

（2）若为椭圆上的动点(异于点),连接并延长交椭圆于点,连接、并分别延

长交椭圆于点连接,设直线、的斜率存在且分别为、,试问是否存在常数,使

得恒成立？若存在,求出的值；若不存在,说明理由.

Answer 1

【答案】(1)；(2)存在，．

【解析】

试题分析：(1)借助题设条件运用向量的相等建立方程组求解；(2)借助题设条件运用直线与椭圆的位置关系联立坐标方程求解.

试题解析：

（1）,化简得,点为线段的中点,, 从而,左焦点,故椭圆的方程为.

（2）存在满足条件的常数.设,

则直线的方程为,代入椭圆方程整理得,.

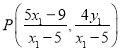,从而,故点.同理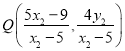,点.因为三点、、共线，所以,从而.

从而,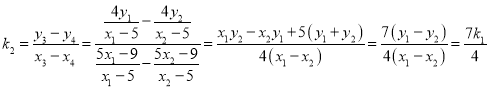

故,从而存在满足条件的常数.