题目内容
已知函数f(x)=(2cos2x-1)sin2x+ cos4x (1)求f(x)的最小正周期及最大值。
cos4x (1)求f(x)的最小正周期及最大值。
(2)设A,B,C为△ABC的三个内角,若cosB=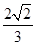 ,f(
,f(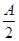 )=-
)=- ,且角A为钝角,求sinC
,且角A为钝角,求sinC
(1) 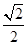 (2)
(2) 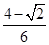
解析(1)f(x)=(2cos2x-1)sin2x+ cos4x
cos4x
=cos2xsin2x+ cos4x
cos4x
= sin4x+
sin4x+ cos4x
cos4x
=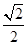 sin(4x+
sin(4x+ )
)
∴最小正周期T=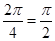
当4x+ =
= +2k
+2k (k∈Z),即x=
(k∈Z),即x=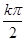 +
+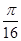 (k∈Z)时,f(x)max=
(k∈Z)时,f(x)max=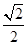
故最小正周期为 ,最大值为
,最大值为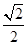 。
。
(2)∵f(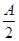 )=-
)=- ,
,
∴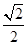 sin(4×
sin(4×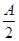 +
+ )=-
)=-
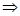 sin(2A+
sin(2A+ )=-
)=-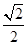
又A为钝角,所以2A+ =
=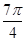 ,即A=
,即A=
由cosB=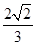 得,sinB=
得,sinB=
又sinC=sin[π-(A+B)]=sin(A+B)=sinAcosB+cosAsinB
=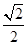 ×
×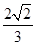 +(-
+(-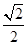 )×
)× =
=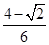

练习册系列答案
相关题目
 是
是 的三个内角,其对边分别为
的三个内角,其对边分别为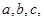 且
且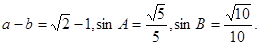
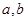 的值; (2)若角A为锐角,求角
的值; (2)若角A为锐角,求角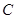 和边
和边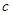 的值.
的值.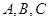 的对边分别为
的对边分别为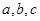 ,且
,且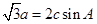 .
.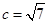 ,且△ABC的面积为
,且△ABC的面积为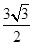 ,求
,求 的值。
的值。 ,求C
,求C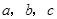 ,已知
,已知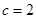 ,
,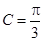 .
. 的面积等于
的面积等于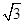 ,求
,求 ;
;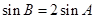 ,求
,求 ,
, ,a=2
,a=2 ,且
,且 ·
· =
=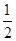 .
.
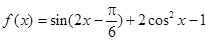 .
. 的单调增区间;
的单调增区间;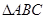 中,
中, 分别是角
分别是角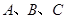 的对边,且
的对边,且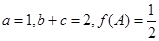 ,求
,求 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,
, ,求
,求 .
.