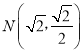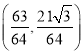题目内容
【题目】为调查中学生平均每人每天参加体育锻炼的时间
（单位：
），按锻炼时间分下列四种情况统计：（1）
；（2）
；（3）
；（4）
以上，有10000名中学生参加了此项活动，下图是此次调查中某一项的流程图，若平均每天参加体育锻炼的时间在
的学生频率是0.15，则输出的结果为________．
【答案】8500
【解析】
分析程序框图，可知输出的S的值是运动时间超过20分钟的学生人数，结合平均每天参加体育锻炼的时间在0~20分钟的时间的学生的频率是0.15，及总人数是10000，运算即得解
由图可知输出的S的值是运动时间超过20分钟的学生人数，由于统计总人数是10000，又平均每天参加体育锻炼的时间在0~20分钟的时间的学生的频率是0.15，由于事件“平均每天参加体育锻炼事件超过20分钟的学生”的频率是1-0.15，
故运动时间不超过20分钟的学生人数是
故答案为：8500
练习册系列答案
超能学典应用题题卡系列答案
相关题目
【题目】某校的一个社会实践调查小组，在对该校学生的良好“用眼习惯”的调查中，随机发放了120分问卷.对收回的100份有效问卷进行统计，得到如
下列联表：
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
（1）现按女生是否能做到科学用眼进行分层，从45份女生问卷中抽取了6份问卷，从这6份问卷中再随机抽取3份，并记其中能做到科学用眼的问卷的份数
，试求随机变量的分布列和数学期望；
（2）若在犯错误的概率不超过
的前提下认为良好“用眼习惯”与性别有关，那么根据临界值表，最精确的的值应为多少？请说明理由.
附：独立性检验统计量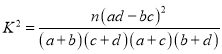
，其中
.
独立性检验临界值表：
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
