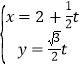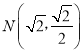题目内容
【题目】已知抛物线C:![]() (
(![]() )的焦点为F,过F且斜率为1的直线与C交于A,B两点,
)的焦点为F,过F且斜率为1的直线与C交于A,B两点,![]() .
.
(1)求C的方程;
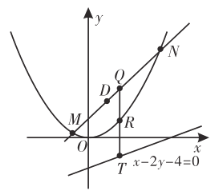
(2)过点![]() 的直线l交C于点M,N,点Q为
的直线l交C于点M,N,点Q为![]() 的中点,
的中点,![]() 轴交C于点R,且
轴交C于点R,且![]() ,证明:动点T在定直线上.
,证明:动点T在定直线上.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)联立直线方程与抛物线方程得到关于x的一元二次方程,利用韦达定理逐步求出![]() 、
、![]() ,再利用弦长公式即可求得p,从而得出抛物线方程;(2)设l方程为
,再利用弦长公式即可求得p,从而得出抛物线方程;(2)设l方程为![]() ,联立直线方程与抛物线方程得到关于x的二次方程,利用韦达定理用k表示出
,联立直线方程与抛物线方程得到关于x的二次方程,利用韦达定理用k表示出![]() 、
、![]() ,即可逐步求出点Q、点R的坐标,由
,即可逐步求出点Q、点R的坐标,由![]() 可求出T点的坐标,消去k即可求得点T所在定直线.
可求出T点的坐标,消去k即可求得点T所在定直线.
(1)设![]() ,
,![]() ,
,
因为![]() ,所以过F且斜率为1的直线方程为
,所以过F且斜率为1的直线方程为![]() ,
,
代入![]() ,得
,得![]() ,
,
所以![]() ,
,
![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以C方程为![]() .
.
(2)证明:因为直线l斜率k存在,设l方程为![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
联立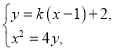
消y得![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
即![]() ,
,
由点R在曲线E上且![]() 轴,
轴,![]() ,得
,得![]() ,R为
,R为![]() 的中点,
的中点,
所以T为![]() ,
,
因为![]() ,所以T在定直线
,所以T在定直线![]() 上.
上.
解法二:(1)同解法一
(2)设![]() ,
,![]() ,
,![]() ,
,
由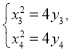 ,作差得
,作差得![]() ,
,
所以![]() ,
,
设![]() ,因为点Q的横坐标
,因为点Q的横坐标![]() ,
,
所以直线![]() 的斜率
的斜率![]() ,又因为
,又因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
因为点R为![]() 的中点,所以
的中点,所以![]() ,
,
因为点R在C上,代入得![]() ,即
,即![]() ,
,
所以T在定直线![]() 上.
上.

【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量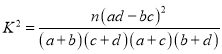 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |